 |
 |
 |
 | Simulating propagation of separated wave modes in general anisotropic media,
Part II: qS-wave propagators |  |
![[pdf]](icons/pdf.png) |
Next: Pseudo-pure-mode qSV-wave equation
Up: Cheng & Kang: Propagate
Previous: Phase velocity and polarization
Pure SH-waves horizontally polarize in the planes perpendicular to the symmetry axis of VTI media with
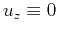 , so we introduce a similarity transformation to the Christoffel matrix
ignoring the vertical component, i.e.,
, so we introduce a similarity transformation to the Christoffel matrix
ignoring the vertical component, i.e.,
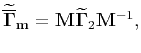 |
(11) |
with a generally invertible 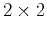 matrix
matrix
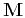 related to the reference polarization direction
related to the reference polarization direction
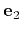 :
:
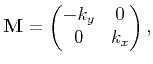 |
(12) |
and
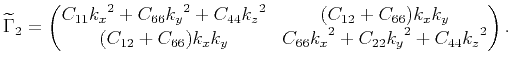 |
(13) |
Accordingly, we derive a transformed Christoffel equation,
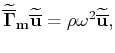 |
(14) |
for the SH-wave mode:
 |
(15) |
in which
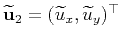 represents the horizontal
components of the original elastic wavefields, and
represents the horizontal
components of the original elastic wavefields, and
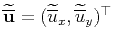 represents the horizontal components of the transformed wavefields.
Note that the matrix
represents the horizontal components of the transformed wavefields.
Note that the matrix
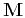 will be not invertible when
will be not invertible when 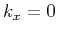 or/and
or/and 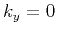 .
These special directions don't affect the derivation of the pseudo-pure-mode wave equation for the following reasons:
First, we don't directly project the elastic wavefield into the wavenumber-domain, but instead apply the similarity transformation to the Christoffel equation
and eventually inverse the transformed Christoffell equation back into the time-space-domain.
Second, the original Christofell matrix
.
These special directions don't affect the derivation of the pseudo-pure-mode wave equation for the following reasons:
First, we don't directly project the elastic wavefield into the wavenumber-domain, but instead apply the similarity transformation to the Christoffel equation
and eventually inverse the transformed Christoffell equation back into the time-space-domain.
Second, the original Christofell matrix
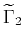 automatically becomes a diagonal matrix in these directions,
so the similarity transformation is not actually needed for the corresponding wavenumber components.
automatically becomes a diagonal matrix in these directions,
so the similarity transformation is not actually needed for the corresponding wavenumber components.
Note the similarity transformation does not change the eigenvalue of the Christoffel
matrix corresponding to the SH-wave and, thus, introduces no kinematic error for this wave mode.
We also can obtain a kinematically equivalent Christoffel equation if
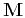 is constructed using
the normalized form of
is constructed using
the normalized form of
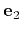 to ensure all spatial frequencies are uniformly scaled.
For a locally smooth medium, applying an inverse Fourier transform to
equation 14, we obtain a linear second-order system in the time-space domain:
to ensure all spatial frequencies are uniformly scaled.
For a locally smooth medium, applying an inverse Fourier transform to
equation 14, we obtain a linear second-order system in the time-space domain:
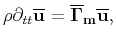 |
(16) |
or in its extended form:
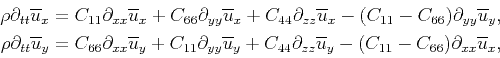 |
(17) |
where
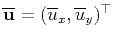 represents the horizontal components of SH-wave in time-space domain, and
represents the horizontal components of SH-wave in time-space domain, and
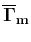 represents the Christoffel differential-operator matrix after the similarity transformation.
represents the Christoffel differential-operator matrix after the similarity transformation.
Due to the cylindrical symmetry of a TI material, the two equations in equation 17 may be summed to
produce a scalar wave equation in terms of
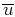 :
:
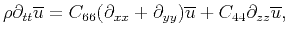 |
(18) |
with
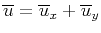 representing the total horizontal components of the transformed SH-wave fields.
This is consistent with the fact that only
representing the total horizontal components of the transformed SH-wave fields.
This is consistent with the fact that only 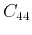 and
and  affect the kinematic signatures of the
SH-wave in VTI media (Tsvankin, 2001). In addition, the derived equation naturally reduces to the acoustic wave equation if we apply the isotropic assumption by setting
affect the kinematic signatures of the
SH-wave in VTI media (Tsvankin, 2001). In addition, the derived equation naturally reduces to the acoustic wave equation if we apply the isotropic assumption by setting
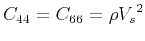 with
with 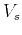 representing the velocity of the isotropic shear wave.
representing the velocity of the isotropic shear wave.
 |
 |
 |
 | Simulating propagation of separated wave modes in general anisotropic media,
Part II: qS-wave propagators |  |
![[pdf]](icons/pdf.png) |
Next: Pseudo-pure-mode qSV-wave equation
Up: Cheng & Kang: Propagate
Previous: Phase velocity and polarization
2016-10-14
![]() is constructed using
the normalized form of
is constructed using
the normalized form of
![]() to ensure all spatial frequencies are uniformly scaled.
For a locally smooth medium, applying an inverse Fourier transform to
equation 14, we obtain a linear second-order system in the time-space domain:
to ensure all spatial frequencies are uniformly scaled.
For a locally smooth medium, applying an inverse Fourier transform to
equation 14, we obtain a linear second-order system in the time-space domain:
![]() :
: