A variational approach for picking optimal surfaces from semblance-like panels

Theory

As a natural extension of the one-dimensional functional of Fomel (2009) (Equation 2) to higher dimensions, consider the functional

$$\tilde{G}[v] = \int_\Omega e^{-\alpha[v(\mathbf{x}),\mathbf{x}]}\... ...\vert^2} + \frac{\epsilon}{2} \left\vert \nabla v \right\vert^2 \right)d\Omega.$$ (4)

In Equation 4, we assume that $\lambda$ and $\epsilon$ are strictly positive real numbers, and $\Omega \subset \mathbb{R}^n$ is a convex, bounded set with Lipschitz boundary $\partial \Omega = \Gamma$ . Possible solutions $v$ exist in the set of real valued functions $V \subset H^1(\Omega)$ , the infinite-dimensional vector space of functions whose gradient components are square integrable, such that $\forall v \in V, \nabla v \cdot \hat{\mathbf{n}} = 0$ for $\hat{\mathbf{n}} \in \Gamma$ , which is equivalent to a zero-flux boundary condition. $\alpha \in C^1(V\times \Omega, [0,\bar{\alpha}])$ with $0<\bar{\alpha}< \infty$ , or $\alpha$ is a continuous function defined for all plausible velocities $v$ in $V$ and at all spatial locations $\mathbf{x}$ in study area $\Omega$ , such that its output is between 0 and some finite positive number $\bar{\alpha}$ . $\alpha[v,\mathbf{x}]$ is assumed to be a Lipschitz continuous function in $v$ such that $\left\vert \alpha_v \right\vert \leq L_{\alpha 1}$ , or the magnitude of its partial derivative with respect to $v$ is bounded by a constant, $L_{\alpha 1}$ . Furthermore, the partial derivative of $\alpha$ in $v$ is also assumed to be Lipschitz continuous with $\left\vert \alpha_{vv} \right\vert \leq L_{\alpha 2}$ , or the magnitude of its second partial derivative with respect to $v$ is bounded by a constant, $L_{\alpha 2}$ . We use $\left\vert \mathbf{x} \right\vert$ to signify $\sqrt{\mathbf{x} \cdot \mathbf{x}}$ for $\mathbf{x} \in \mathbb{R}^n$ , which reduces to the absolute value function if $x\in \mathbb{R}$ . We wish to find the $v \in V$ that minimizes this equation and will serve as the picked velocity model.

$\alpha$ is a semblance-like volume over spatial domain $\Omega$ . $\lambda$ and $\epsilon$ are regularization parameters. Increasing $\lambda$ makes the minimizing functions more closely follow highs in $\alpha$ , while decreasing it makes the output minimizing functions smoother. $\epsilon$ is a small positive term which penalizes changes in minimizing functions and ensures they exists in $H^1(\Omega)$ (Dobson and Vogel, 1997). Although we found that $\epsilon$ may be set to negligibly small values on the order of machine precision in practice, a complete mathematical treatment of this problem, which is beyond the scope of this manuscript but may be found in Chapter 5 of Decker (2021) and draws inspiration from Dacorogna (2004) and Smyrlis and Zisis (2004), shows how the $\epsilon$ term is essential for guaranteeing the existence of and convergence to minimizers of Equation 4 in an infinite-dimensional setting. Again, larger values of $\lambda$ lead to minimizing surfaces which may vary significantly to follow high values of $\alpha$ more closely. Larger values of $\epsilon$ ensure that minimizing surfaces have less total variation. The examples in this paper use $1 \leq \lambda \leq 5$ and $\epsilon = 10^{-3}$ .

Minimizing surfaces of Equation 4 occur when its Fréchet derivative, defined as

$$\begin{split}\nabla \tilde{G}(v) =& -\alpha_v[v(\mathbf{x}),\... ... v\right\vert^2}}+\epsilon \right]\nabla v \right), \end{split}$$ (5)

is equal to zero. In the right-hand side of Equations 4 and 5, gradient and divergence operations are applied in $\mathbf{x} \in \Omega$ , where $\Omega \subset \mathbb{R}^n$ is the domain of velocity models, and are based on derivatives for each spatial dimension of $\mathbf{x}$ . On the left-hand side of Equation 5, the gradient operation refers to the functional gradient, which is applied to a functional $\tilde{G}[v]$ which maps $v \in H^1(\Omega)$ to a real number. This functional gradient, $\nabla \tilde{G}[v]$ , is itself a function defined on $\Omega$ .

Directly determining minimizing surfaces involves solving a nonlinear elliptic partial differential equation, which can be challenging. Instead, we choose to adopt an iterative approach by introducing a pseudo-time coordinate, $\tau$ , and solving the parabolic equation

$$\frac{\partial v}{\partial \tau} = -\nabla \tilde{G}(v),$$ (6)

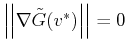by allowing $v$ to evolve in $\tau$ until it converges to a critical $v^\ast$ where $\left\vert\left\vert\nabla \tilde{G}(v^\ast)\right\vert\right\vert=0$ . This is a common approach for finding the minima of a functional (Mawhin and Willem, 2010) and suggests the use of an iterative gradient descent scheme. This method provides a sequence $\{v_i\}_{i\in\mathbb{N}}$ of subsequent approximations for $v^\ast$ , the critical point of $\tilde{G}(v)$ . The update structure given an initial velocity model function $v_0$ is

$$v_{i+1} = v_i + \rho_i h_i ,$$ (7)

where $v_i$ are updated velocity models and $h_i$ are search directions. Control parameters, also known as step sizes, $\{\rho_i\}_{i\in\mathbb{N}}$ satisfy $a \leq \rho_i \leq b$ for positive real numbers $a,b$ whose values are related to the smoothness of $\alpha$ (Decker, 2021). Experiments in this paper use $a=10^{-8}$ and $b=10^{-2}$ . At each step in Equation 7, $\nabla \tilde{G}(v_i)$ is evaluated. 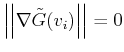If $\left\vert\left\vert\nabla \tilde{G}(v_i)\right\vert\right\vert = 0$ the method stops because it has arrived at a critical point or minimizer. Otherwise, 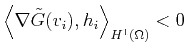$h_i$ is chosen to satisfy $\left<\nabla \tilde{G}(v_i),h_i\right>_{H^1(\Omega)}<0$ , where $\left< \cdot , \cdot \right>_{H^1(\Omega)}$ is the $H^1$ inner product on $\Omega$ . In the method of steepest descent $h_i = -\nabla \tilde{G}(v_i)$ . $v_{i+1}$ is computed and the method proceeds to the next step. Example pseudocode for a picking algorithm using continuation can be found in Appendix .

An iterative algorithm for minimizing Equation 4 to pick an optimal surface from a semblance-like volume is implemented in the Madagascar software library (Fomel et al., 2013) using NumPy. Parallelism is achieved using Numba, and NumPy functions are rewritten as simple, array-based, object-free operations and performance tested using Numba on a Texas Advanced Computing Center (TACC) Stampede2 compute node with 48 Skylake cores for code optimization of each component helper function. The Fréchet derivative, or functional gradient $\nabla \tilde{G}(v)$ , given by Equation 5 is computed using finite-difference derivative operations and the Numba functions written for the task. The finite-difference approach was chosen for numerical efficiency. Representing the large, semblance-like panels that are used for $\alpha[v(\mathbf{x}),\mathbf{x}]$ as FEniCS interpolated functions for finite element implementation was found to be overly expensive, and finite-difference computations yielded satisfactory results at reduced computational cost. The calculated gradient is utilized with the $\ell$ -BFGS two-loop recursion method outlined by Nocedal (1980) for approximating the inverse Hessian and calculating a search direction. After experimentation on different data sets, we found that a memory size of the past 3 gradient computations for use in the approximation of the inverse Hessian achieved the most rapid cost convergence results. The step size is determined using the output search direction with a golden-section search (Mordecai and Wilde, 1966; Kiefer, 1953). The method is allowed to iterate and update the model until either a maximum number of iterations are achieved, any step size in the search direction fails to decrease the cost by more than a set amount, or the $L^2$ magnitude of the calculated gradient drops below a threshold. We also found that the Hessian may change rapidly in this problem, leading some search directions output by the $\ell$ -BFGS scheme to increase the cost of surfaces for all step sizes. In this circumstance, the previous gradient computations are ``forgotten'' and the $\ell$ -BFGS algorithm is reset, enabling a fresh approximation of the inverse Hessian. Careful readers will also notice a dimensional analysis ambiguity when calculating best-fit surfaces from typical semblance panels using the Fréchet derivative defined in Equation 5. Usually, the first axis in these data is seismic trace recording time, while other axes are spatial with units of distance. In order to convert derivatives in these different units into similar ones, spatial derivatives are multiplied by the velocity model for the previous iteration so they have units of s$^{-1}$ .

Convergence of this algorithm requires at least local convexity (Li and Fukushima, 2001; Nocedal, 1980; Dennis and Moré, 1977), which is achieved by enforcing smoothness on $\alpha[v(\mathbf{x}),\mathbf{x}]$ using triangle smoothing filters (Claerbout, 1993). As a practical point, artificially large values in $\alpha[v(\mathbf{x}),\mathbf{x}]$ not related to high-quality fit for the parameter being tested must be muted to prevent them from capturing the cost minimizing surface. In this paper, we manually define muting functions.

Convergence can only be guaranteed to a local minimizer. For a unique minimizer to exist, the integrand of Equation 4 would need to be strictly convex in every $v$ , $\nabla v$ combination for all $\mathbf{x} \in \Omega$ (Dacorogna, 2004), which places unrealistic burdens on $\alpha$ . In order to overcome the multimodality of this problem, we employ continuation, or graduated optimization. This involves smoothing and scaling the semblance-like volume several times. Smoothing makes the semblance volume more convex, and scaling increases the attraction of semblance highs for $v(\mathbf{x})$ surfaces. If sufficiently strong smoothing is applied, the problem may become convex (Hazan et al., 2016). In this paper, the authors choose a set of minimum smoothing radii that capture the finest scale of changes in the semblance-like volume that appear to be representative of the underlying model. The maximum smoothing radii are determined by multiplying the minimum radii by a sufficiently large number so that smoothing makes panels of the semblance volume appear strictly convex. We choose a number of smoothing levels, then proceed incrementally from maximum to minimum smoothing in a linear manner. The semblance scaling factor for each level is chosen to be proportional to the ratio between smoothing at that level and minimum smoothing. A constant-gradient velocity field is used as the starting model on the most-smoothed semblance volume, and the minimizing velocity surface is iteratively determined using the two-loop recursion $\ell$ -BFGS scheme until convergence on that model is achieved. The minimizing surface from one level of smoothing is then used as the starting model on the next-less-smoothed semblance volume. The method proceeds until finding the cost minimizing velocity on the least-smoothed model. Because the method is allowed to operate on semblance-like volumes with different levels of smoothing, it is able to find the macro-trends for the best-fit surface before determining finer components. This enables the method to behave more like a global optimizer and enjoy applicability to problems beyond picking velocity surfaces from semblance-like volumes as experiments in subsequent sections illustrate.

A variational approach for picking optimal surfaces from semblance-like panels