|
|
|
|
Plane-wave Sobel attribute for discontinuity enhancement in seismic images |
|
|---|
|
penobs
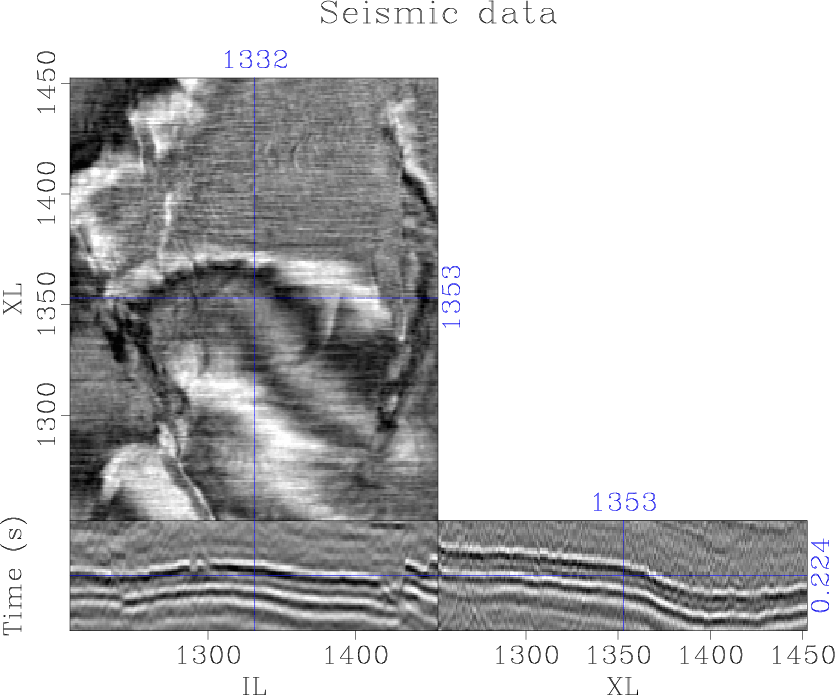
Figure 4. The Penobscot seismic data |
|
|
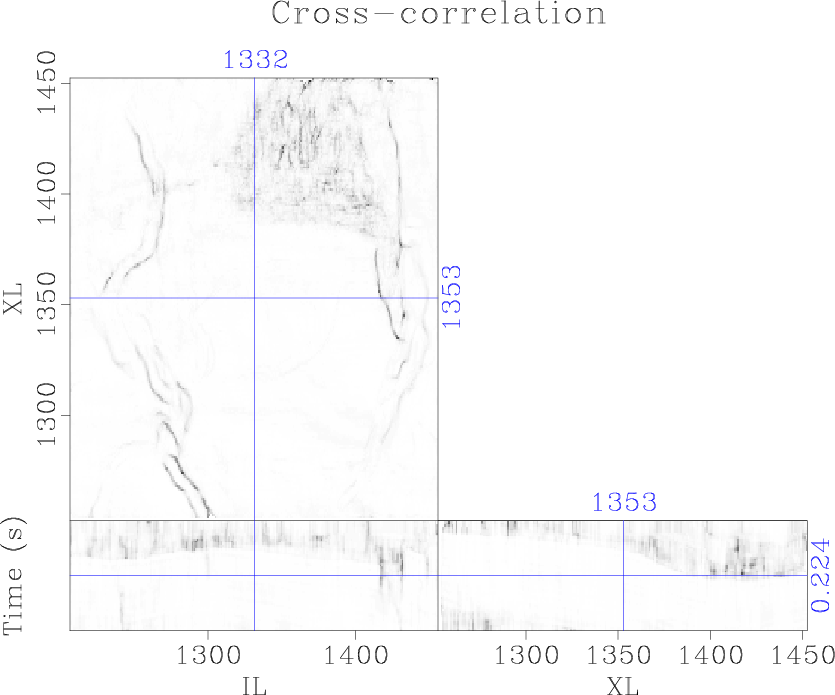
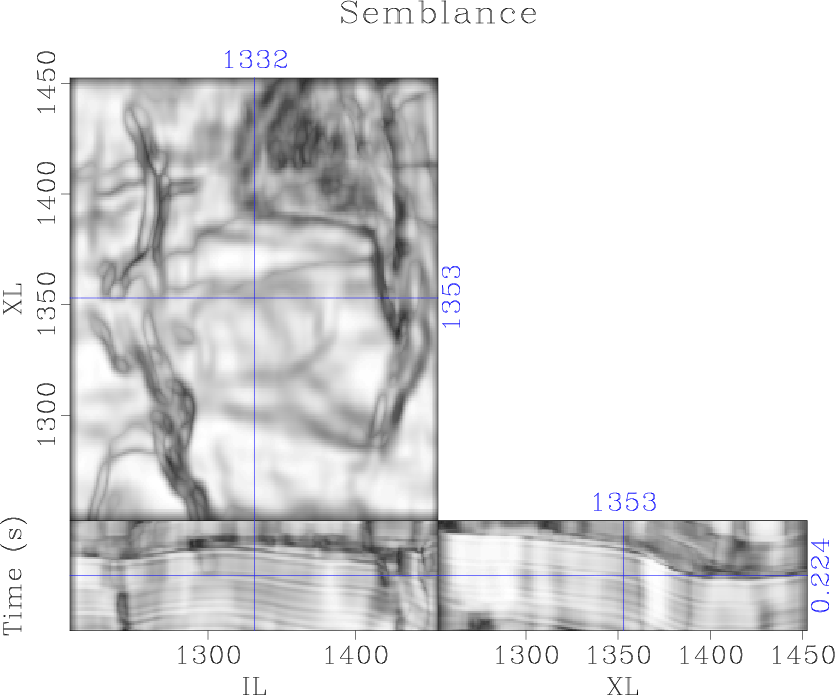
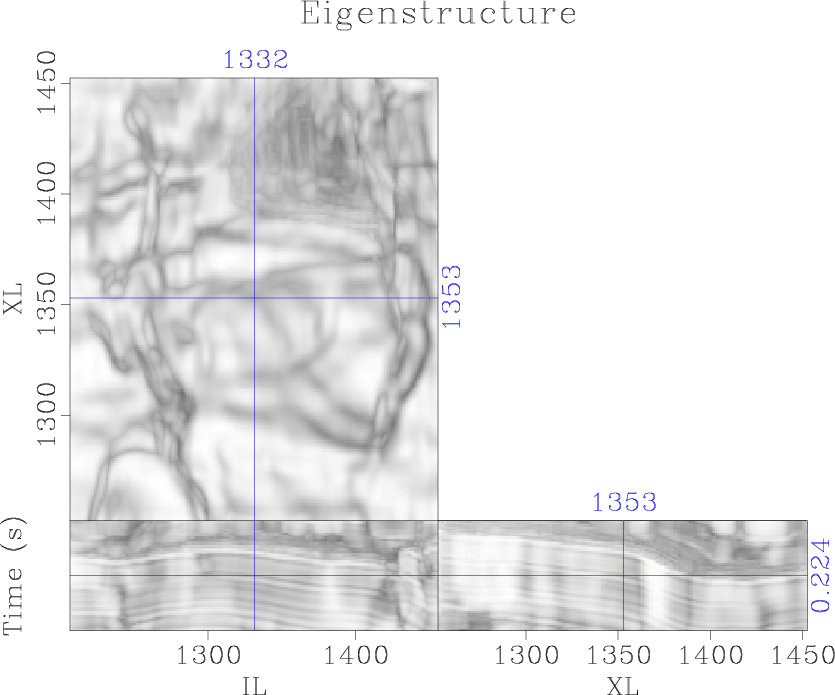
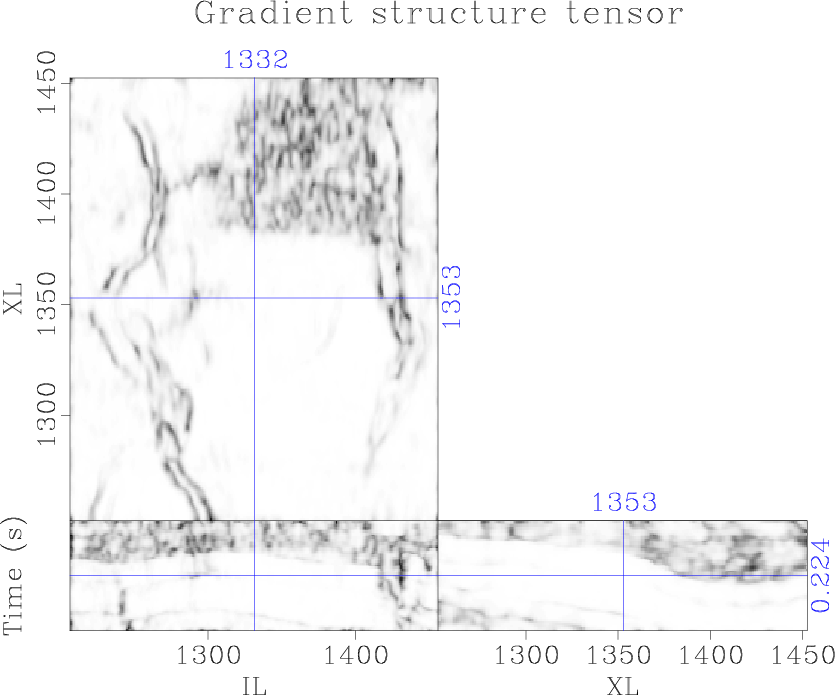
We apply cross-correlation coherence, semblance, eigenstructure coherence, and gradient-structure-tensor (GST) coherence attributes to the data and compare the results to the proposed plane-wave Sobel attributes. Correlation-based coherence attributes (Bahorich and Farmer, 1995) produce an image of normalized local cross-correlation between adjacent seismic traces and combines them to estimate coherence. This attribute is more efficient than most of the alternative coherence attributes, but lacks robustness and has poor vertical resolution (Figure 6a). Semblance (Marfurt et al., 1998) provides better vertical resolution by incorporating a local window of traces (Figure 6b). Eigendecomposition of the local covariance matrix (Gersztenkorn and Marfurt, 1999) or gradient-structure-tensor (Randen et al., 2000) allows information about local structures to be incorporated into the coherence calculation. These attributes provide significantly better vertical and lateral resolution (Figures 6c and 6d) compared to correlation-based coherence; however, calculation and decomposition of the local covariance matrix or gradient-structure-tensor introduces significant computational cost. Furthermore, all of these attributes contain some noise contamination in coherent sections of the image.
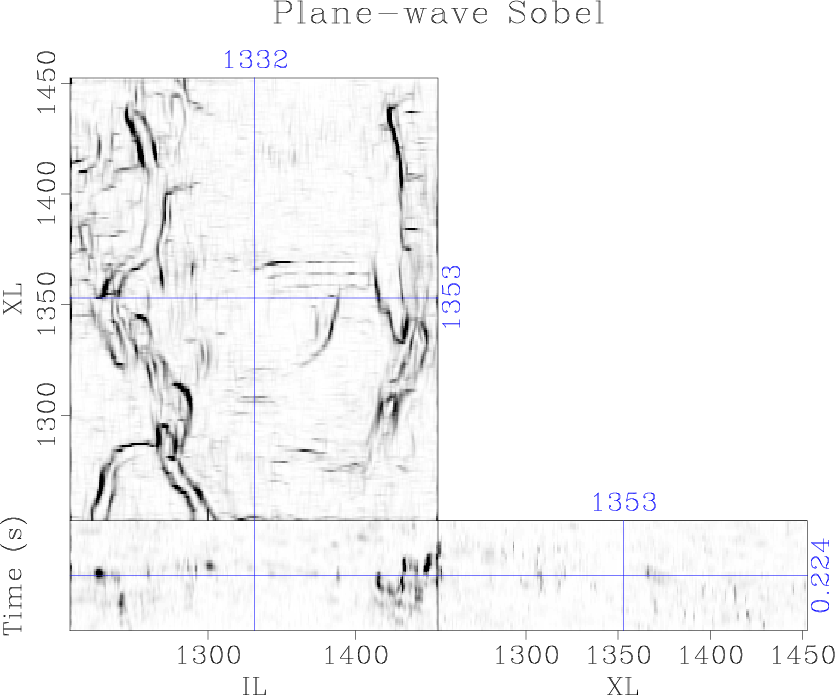
We compare these results to the proposed plane-wave Sobel attributes. As expected, the filter enhances the faults and channels in the seismic image without significant noise contamination or highlighting continuous dipping reflectors (Figure 5f).
As previously stated, computational efficiency is one of the key advantages of the plane-wave Sobel attribute. Though all of the discussed algorithms are straightforward to parallelize, we compare the attributes on a single core computer for simplicity (Table 1). We find that the plane-wave Sobel attributes significantly outperform many popular coherence attributes. Admittedly, commercial implementations may be more efficient than our implementation.
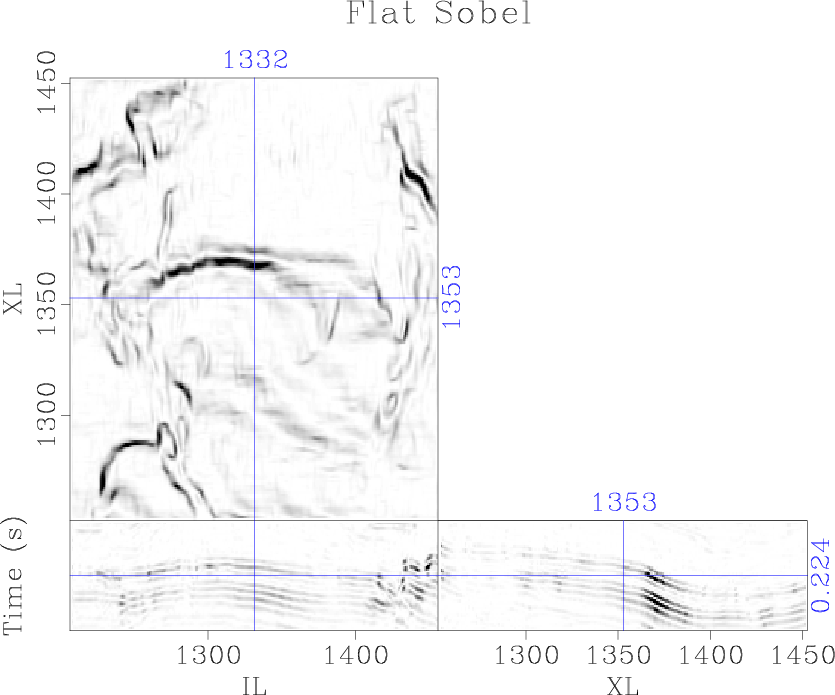
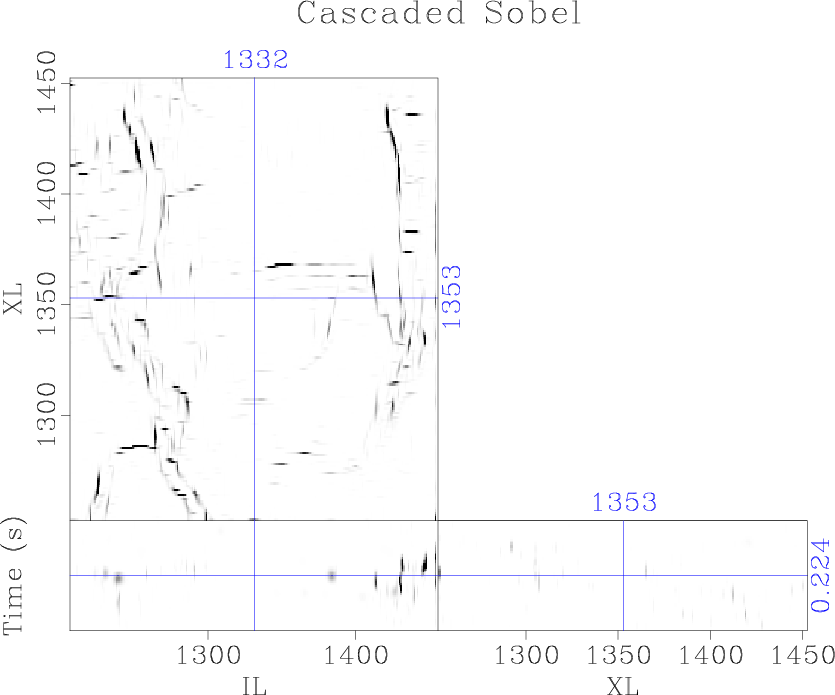
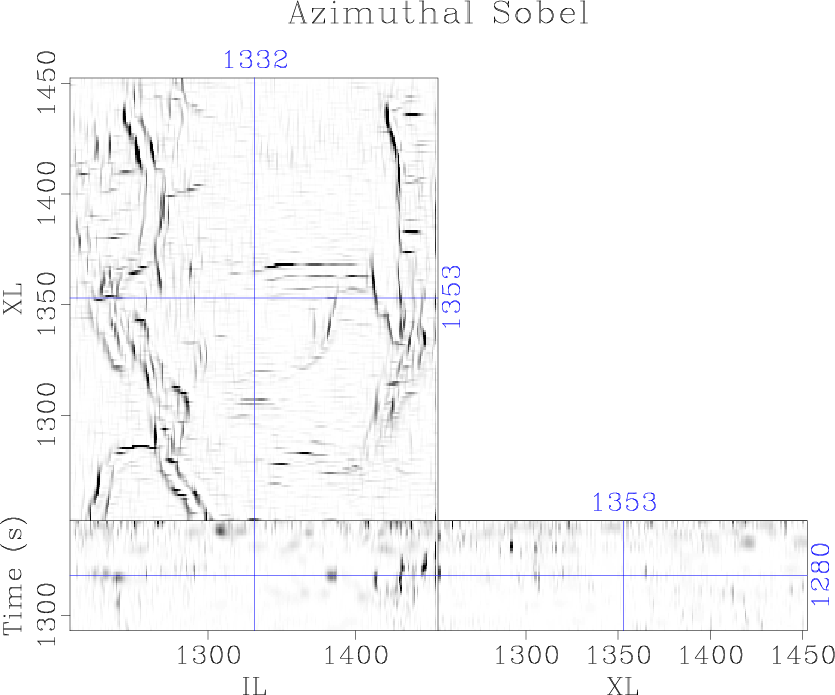
The plane-wave Sobel attribute (Figure 5b) is capable of providing interpreters with a detailed image of seismic discontinuities in a fraction of the time of conventional coherence attributes, expediting the interpretation process. Computation of the cascaded Sobel attribute (Figure 5c) and azimuthal Sobel attribute (Figure 5d) may not provide significantly more value to the interpreter, as many of the same features can be interpreted from the less expensive plane-wave Sobel image; however, these attributes are significantly more segmented and may be good inputs to automatic fault plane interpretation algorithms.
|
|---|
|
s,sobel,sobel2,slices
Figure 5. Comparison of (a) the traditional Sobel filter, (b) proposed plane-wave Sobel filter, (c) cascaded plane-wave Sobel filter, and (d) azimuthal plane-wave Sobel filter |
|
|
|
|---|
|
coh0,coh1,coh2,coh
Figure 6. Comparison of discontinuity enhancement attributes: (a) cross-correlation, (b) semblance, (c) eigenstructure, and (d) gradient-structure tensor |
|
|
| Attribute | Compute time |
| Flat Sobel | 0.3 seconds |
| Gradient structure tensor | 4 seconds |
| Plane-wave Sobel | 17 seconds |
| Cascaded Sobel | 21 seconds |
| Predictive | 40 seconds |
| Azimuthal Sobel | 3 minutes |
| Cross-correlation | 5 minutes |
| Semblance | 1 hour |
| Eigenstructure | 3 hours |
|
|
|
|
Plane-wave Sobel attribute for discontinuity enhancement in seismic images |