Random noise attenuation using local signal-and-noise orthogonalization

Compensating for the signal-leakage energy by weighting

For many random noise attenuation approaches, the leakage energy is not negligible. We can attempt to retrieve the leaking signal from the noise section by applying a simple nonstationary weighting operator to the initially denoised signal assuming that the leakage energy can be predicted by weighting the useful signal:

$$\mathbf{s}_1=\mathbf{w}\circ \mathbf{s}_0.$$ (1)

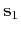Here $\mathbf{s}_1$ is the retrieved signal, 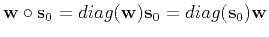$\mathbf{w}\circ\mathbf{s}_0=diag(\mathbf{w})\mathbf{s}_0=diag(\mathbf{s}_0)\mathbf{w}$ , which denotes Hadamard (or Schur) product, and 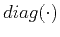$diag(\cdot)$ denotes the diagonal matrix composed of an input vector. The weighting vector 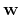$\mathbf{w}$ can be estimated by solving the following minimzation problem:

$$\min_{\mathbf{w}} \parallel \overbrace{\mathbf{d} - \mathbf{P}[\m... ...mathbf{w}\circ \overbrace{\mathbf{P}[\mathbf{d}]}^{\mathbf{s}_0} \parallel_2^2,$$ (2)

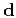where $\mathbf{d}$ denotes the observed noisy data, and 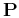$\mathbf{P}$ denotes the initial random noise attenuation operator. Equation 2 uses a weighted (scaled) signal 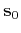$\mathbf{s}_0$ to match the leakage energy in the initial noise section ( 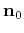$\mathbf{n}_0$ ) in a least-squares sense. In the next section, we will introduce an approach to calculate the weighting vector 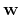$\mathbf{w}$ using local orthogonalization.

Random noise attenuation using local signal-and-noise orthogonalization