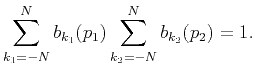|
 |
 |
 | Omnidirectional plane-wave destruction |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Chen, Fomel & Lu:
Previous: Acknowledgment
Appendix: Separability of the 2D maxflat filter
Following Thiran (1971),
the maxflat condition of 1D fractional delay
filter
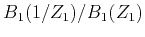 is expressed as
is expressed as
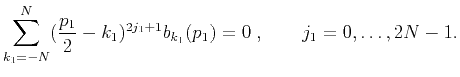 |
(22) |
With the additional constraint (Chen et al., 2013)
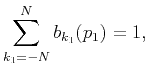 |
(23) |
we can obtain the unique
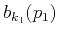 .
Similarly,
.
Similarly,
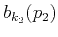 satisfies
the following linear system:
satisfies
the following linear system:
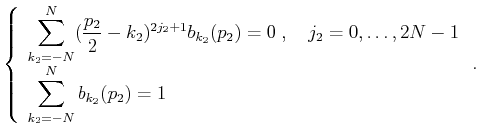 |
(24) |
Substituting
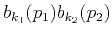 into
the 2D maxflat equation 12, for all
into
the 2D maxflat equation 12, for all
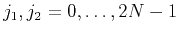 , we obtain
, we obtain
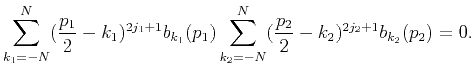 |
(25) |
Also, for
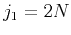 , and
, and
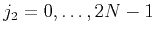 or
or  , and
, and
 ,
equation 12 still holds true.
,
equation 12 still holds true.
Substituting
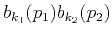 into
the additional constraint in Equation 13,
into
the additional constraint in Equation 13,
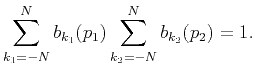 |
(26) |
In other words,
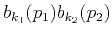 is a solution of
the combined linear system of equation 12 and 13.
This linear system must have a unique solution, therefore
is a solution of
the combined linear system of equation 12 and 13.
This linear system must have a unique solution, therefore
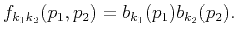 |
(27) |
 |
 |
 |
 | Omnidirectional plane-wave destruction |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Chen, Fomel & Lu:
Previous: Acknowledgment
2013-08-09
![]() is expressed as
is expressed as
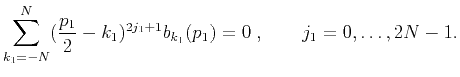
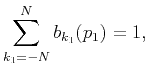
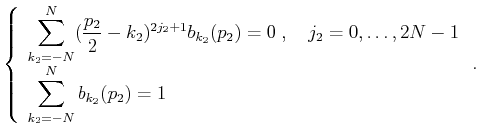
![]() into
the 2D maxflat equation 12, for all
into
the 2D maxflat equation 12, for all
![]() , we obtain
, we obtain
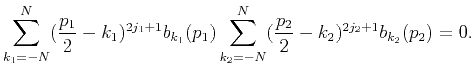
![]() into
the additional constraint in Equation 13,
into
the additional constraint in Equation 13,