|
|
|
|
Selecting an optimal aperture in Kirchhoff migration using dip-angle images |
One approach to analyzing constant-dip partial-image consistency is to measure the local slope in every partial image and to construct a taper function that is based on this measurement. The taper should protect events whose slope is close to the corresponding constant dip. Slopes that differ significantly from that of the constant dip should be attenuated. However, if conflicting dips occur in the partial image, dips estimation becomes a non-trivial task.
To avoid this issue, we estimate segment conformity with a partial image by stacking along a local trajectory defined by partial-image constant dip. Constructive segments match the trajectory that yields high values of coherency. On the other hand, destructive segments get stacked in the wrong direction and provide low values of coherence. Classic semblance (Taner and Koehler, 1969), as a coherence measure, can be used for defining a weight function. Weighting of migrated data corresponds to migration aperture optimization.
For illustration, we use the constant-dip partial images shown in Figure 9. They correspond to migration dips of 0 and 15 degrees,
and we first apply local stacking along directions corresponding to 0 and 15 degrees, respectively. We extend stacking to the dip-angle direction
as well. Effective contributions are locally plane in this direction, and local stacking along migration dips allows for signal enhancement.
We measure coherency of the stacked data and get the semblance function
![]() presented in Figure 10.
High semblance values correspond to events consistent with the dips of partial images. The next step is to transform the semblance function
to a weight function
presented in Figure 10.
High semblance values correspond to events consistent with the dips of partial images. The next step is to transform the semblance function
to a weight function
![]() , which should optimally handle migrated amplitudes. The weight should not change a plane diffraction
event or an effective apex area of reflections. At the same time, the weight should smoothly attenuate away from the apexes so that
edge effects can be eliminated (Hertweck et al., 2003). We define our weight function using the following thresholding rule:
, which should optimally handle migrated amplitudes. The weight should not change a plane diffraction
event or an effective apex area of reflections. At the same time, the weight should smoothly attenuate away from the apexes so that
edge effects can be eliminated (Hertweck et al., 2003). We define our weight function using the following thresholding rule:
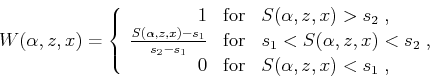 |
(10) |


|
|---|
|
semb-0,semb-15
Figure 10. Semblance function for (a) zero-degree partial image and (b) fifteen-degree partial image. |
|
|
In our synthetic example, we used a dip-angle window of 10 degrees, a lateral window of 150 m, and parameters ![]() and
and ![]() equal to 0.2 and 0.4, respectively. Figure 11 shows the weighted
partial images. Reflectors consistent with the partial images, as well as appropriate parts of the diffraction event, are preserved.
At the same time, a large amount of noneffective contribution, which may produce migration noise, has been eliminated.
Summation of the weighted partial images provides the stacked image, which has the migration artifacts being suppressed significantly
(Figure 12).
equal to 0.2 and 0.4, respectively. Figure 11 shows the weighted
partial images. Reflectors consistent with the partial images, as well as appropriate parts of the diffraction event, are preserved.
At the same time, a large amount of noneffective contribution, which may produce migration noise, has been eliminated.
Summation of the weighted partial images provides the stacked image, which has the migration artifacts being suppressed significantly
(Figure 12).


|
|---|
|
dpis-cln-0,dpis-cln-15
Figure 11. (a) Zero-degree partial image and (b) fifteen-degree partial image after migration-aperture optimization. |
|
|

|
|---|
|
res-clean
Figure 12. Image and dip-angle gather after migration-aperture optimization by slope-consistency analysis. |
|
|
A weight function constructed by using the dip-angle direction only allows for attenuating reflection events around their apex areas while preserving diffraction events as well. Figure 13 shows the result of migrated data weighting using local summation along dip-angle window of 10 degrees. Reflection events are localized around their effective areas, and the diffraction event has its full width being preserved. However, the image remains contaminated by migration artifacts, which happen to be stationary in the dip-angle direction.

|
|---|
|
res-clean1
Figure 13. Image and dip-angle gather after migration-aperture optimization by local summation in the dip-angle direction. |
|
|
We next address the situation when migration velocity is not correct. Figure 14 shows the image and the dip-angle gather after migration with 10% lower velocity. Reflection boundaries look distorted. The diffractor is undermigrated and has a complicated shape in the dip-angle gather. The image is contaminated by strong migration artifacts. For migration-aperture optimization by slope-consistency analysis, we used the same parameters as in the previous example (Figure 15). Reflection and diffraction events both are optimized to their effective parts, eliminating migration noise in the image.

|
|---|
|
fres-init
Figure 14. Initial image and common-image-gather in dip-angle domain corresponding to distance of 7 km (wrong velocity case). |
|
|

|
|---|
|
fres-clean
Figure 15. Image and dip-angle gather after migration-aperture optimization by slope-consistency analysis (wrong velocity case). |
|
|
These experiments demonstrate that slope-consistency filtering can be used after migration even when using a complicated velocity model or an incorrect model. In the previous section, we considered theoretically the case of the zero-offset migration. The proposed principles may apply also to prestack migration in which stacking of the full offset range provides accumulation of effective migrated data parts. The experiments also reveal that noneffective segments may have an appropriate slope as well. For instance, the optimized fifteen-degree partial image (Figure 11b) has some events at a depth of 1.5 km. These events appear to have a correct slope that is close to 15 degrees, and they therefore evade nonconsistent-slope filtering and bring noise to the image of the flat reflector. This kind of noise is inherent in Kirchhoff migration and is produced by the complexity of the velocity model and incompleteness of the migrated data (Stolk and Symes, 2004). In practice, it can be eliminated by stacking the full range of offsets.
The proposed approach can be used easily in three dimensions, in which migrated events are defined by two orthogonal directions (Klokov and Fomel, 2012). Migrated constant-dip traces compose a 3D volume, and slope-consistency analysis should be performed along a plane surface whose slope is defined by the two migration dips. The method does not require slope estimation and has a relatively low computational cost.
Note that the effectiveness of the method is conditioned to that of semblance estimation. In the case of conflicting events, semblance operator effectively deals with events that are relatively strong to be detected. In practice, weak diffraction events might get suppressed by reflections and noise, which might cause difficulties in the slope-consistency estimation and, consequently, in the events protection. These weak events can be enhanced by diffraction imaging techniques (Fomel et al., 2007; Klokov and Fomel, 2012).
|
|
|
|
Selecting an optimal aperture in Kirchhoff migration using dip-angle images |