Equation 27 can be written as a matrix form:
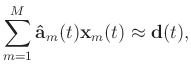 |
(36) |
where
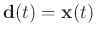 ,
,
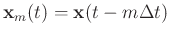 is the time shift
of the input signal
is the time shift
of the input signal
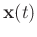 and
and
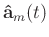 is the time-dependant coefficients.
We solve the under-determined linear system by using the shaping regularization method.
The solution is the form below:
is the time-dependant coefficients.
We solve the under-determined linear system by using the shaping regularization method.
The solution is the form below:
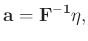 |
(37) |
where
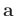 is a vector of
is a vector of
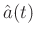 , the elements of vector
, the elements of vector
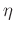 is:
is:
![$\displaystyle \mathbf{\eta}_i(t) = \mathbf{S}\left[\mathbf{x}_i^*(t)\mathbf{d}(t)\right],$](img97.png) |
(38) |
the elements of the matrix
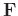 is:
is:
![$\displaystyle \mathbf{F}_{ij}= \sigma^2 \mathbf{\delta}_{ij} + S[\mathbf{x}_i^*(t)\mathbf{x}_j(t) - \sigma^2 \mathbf{\delta}_{ij}]$](img98.png) |
(39) |
where 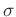 is the regularization parameter,
is the regularization parameter,
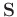 is a shaping operator,
and
is a shaping operator,
and
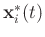 stands for the complex conjugate of
stands for the complex conjugate of
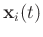 .
We can use the conjugate gradient method to find the solution of the linear system.
The NPM (Fomel, 2013) can be summarized as follows:
.
We can use the conjugate gradient method to find the solution of the linear system.
The NPM (Fomel, 2013) can be summarized as follows:
![\begin{algorithm}{Algorithm 2: non-stationary Prony method}{}
\text{Find time d...
...m=1}^M \hat{A}_m[n]e^{j\hat{\phi}_m[n]}=\sum_{m=1}^M\hat{c}_m[n]
\end{algorithm}](img101.png)
After we decompose the input signal into narrow-band components,
we compute the time-frequency distribution of the input signal
using the Hilbert transform of the intrinsic mode functions.
2020-07-18
![\begin{algorithm}{Algorithm 2: non-stationary Prony method}{}
\text{Find time d...
...m=1}^M \hat{A}_m[n]e^{j\hat{\phi}_m[n]}=\sum_{m=1}^M\hat{c}_m[n]
\end{algorithm}](img101.png)