3D generalized nonhyperboloidal moveout approximation

Nonhyperboloidal moveout approximation

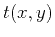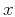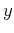Let $t(x,y)$ represent the two-way reflection traveltime as a function of the source-receiver offset with components $x$ and $y$ in a given acquisition coordinate frame. We propose the following general functional form of nonhyperboloidal moveout approximation (Sripanich and Fomel, 2015a):

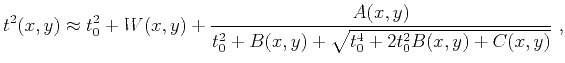$$t^2(x,y) \approx t^2_0 + W(x,y) + \frac{A(x,y)}{t^2_0+B(x,y)+\sqrt{t^4_0+2t^2_0B(x,y)+C(x,y)}} ~,$$ (1)

where

$$W(x,y) = W_1x^2+ W_2xy+ W_3y^2~,$$

$$A(x,y) = A_1x^4+A_2x^3y+A_3x^2y^2+A_4xy^3+A_5y^4~,$$

$$B(x,y) = B_1x^2+B_2xy+B_3y^2~,$$

$$C(x,y) = C_1x^4+C_2x^3y+C_3x^2y^2+C_4xy^3+C_5y^4~,$$

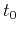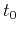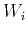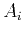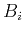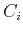and $t_0$ denotes the two-way traveltime at zero offset. The total number of independent parameters in equation 1 is seventeen including $t_0$ , $W_i$ , $A_i$ , $B_i$ , and $C_i$ . A simple algebraic transformation of equation 1 leads to the following expression in polar coordinates:

$$t^2(r,\alpha) \approx t^2_0 + W_r(\alpha) r^2 +$$ (2)

$$\frac{A_r(\alpha) r^4}{t^2_0+B_r(\alpha) r^2+\sqrt{t^4_0+2t^2_0B_r(\alpha) r^2+C_r(\alpha) r^4}} ~,$$

where

$$W_r(\alpha) = \frac{1}{V^2_{nmo}(\alpha)} = W_1\cos^2 \alpha+W_2\cos \alpha \sin \alpha + W_3\sin^2 \alpha~,$$

$$A_r(\alpha) = A_1\cos^4 \alpha+A_2\cos^3 \alpha \sin \alpha+A_3\cos^2 \alpha \sin^2 \alpha+$$

$$A_4\cos \alpha \sin^3 \alpha+A_5\sin^4 \alpha~,$$

$$B_r(\alpha) = B_1\cos^2 \alpha+B_2\cos \alpha \sin \alpha+B_3\sin^2 \alpha~,$$

$$C_r(\alpha) = C_1\cos^4 \alpha+C_2\cos^3 \alpha \sin \alpha+C_3\cos^2 \alpha \sin^2 \alpha+$$

$$C_4\cos \alpha \sin^3 \alpha+C_5\sin^4 \alpha~,$$

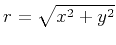and $r=\sqrt {x^2+y^2}$ represents the absolute offset and 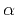$\alpha$ denotes the azimuthal angle from the 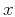$x$ -axis. Along a fixed azimuth 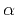$\alpha$ , equation 1 reduces to the generalized nonhyperbolic moveout approximation (GMA) of Fomel and Stovas (2010).

3D generalized nonhyperboloidal moveout approximation