|
|
|
|
On anelliptic approximations for qP velocities in TI and orthorhombic media |
| Parameters | ||||
| 87.11 | 0.467 | 105.39 | 25.19 | |
| 0.005 | 0.649 | 0.20 | ||
| 181.74 | 22.54 | |||
| 13.16 |
| Parameters | ||||
| 0.576 | 0.143 | 0.651 | 0.599 | |
| 0.538 | 0.257 | 1.061 | ||
| 1.325 | 1.279 | |||
| 4.124 |
Table 10 shows a significantly larger correlation between the change in phase velocity with ![]() in comparison with that of
in comparison with that of ![]() , which agrees with the general assumption of the independency of
, which agrees with the general assumption of the independency of ![]() in qP velocities approximations. Likewise, the effect from
in qP velocities approximations. Likewise, the effect from ![]() has a higher correlation with the change of phase velocity than
has a higher correlation with the change of phase velocity than ![]() because the exact qP phase-velocity formula (equation 9) can be expressed in terms of Thomsen parameters with
because the exact qP phase-velocity formula (equation 9) can be expressed in terms of Thomsen parameters with ![]() corresponding to the lower order of
corresponding to the lower order of
![]() than
than ![]() . Moreover,
. Moreover, ![]() and
and ![]() also have high correlation with
also have high correlation with ![]() , which is apparent from their definitions.
, which is apparent from their definitions.
Table 11 shows relatively similar correlations from ![]() and
and ![]() to the change in exact phase velocity suggesting a more symmetric contribution from both parameters. The dimensionless anelliptic parameters
to the change in exact phase velocity suggesting a more symmetric contribution from both parameters. The dimensionless anelliptic parameters ![]() and
and ![]() exhibit a strong correlation, which is consistent with the relationships shown in Figure 1.
exhibit a strong correlation, which is consistent with the relationships shown in Figure 1.
By ignoring the effect of ![]() in the case of Thomsen parameters or using the relationship between
in the case of Thomsen parameters or using the relationship between ![]() and
and ![]() (Figure 1) to reduce the number of parameters to three, we can transform the matrix
(Figure 1) to reduce the number of parameters to three, we can transform the matrix ![]() from
from ![]() to
to ![]() (
(
![]() ). Note that the matrix for Thomsen parameters is similar to Table 10 with the omittance of the row and column associated with
). Note that the matrix for Thomsen parameters is similar to Table 10 with the omittance of the row and column associated with ![]() . Table 12 shows the three-parameter matrix for anelliptic parameters with similar behavior of relatively equal correlations from
. Table 12 shows the three-parameter matrix for anelliptic parameters with similar behavior of relatively equal correlations from ![]() and
and ![]() as before.
as before.
| Parameters | ||||
| 0.578 | 0.144 | 1.166 | ||
| 0.534 | 1.286 | |||
| 7.411 |
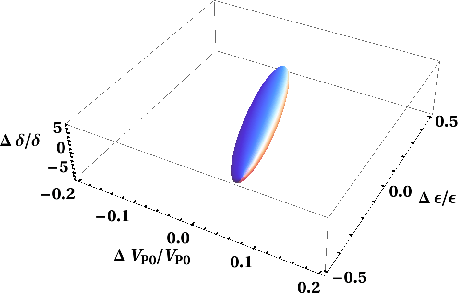
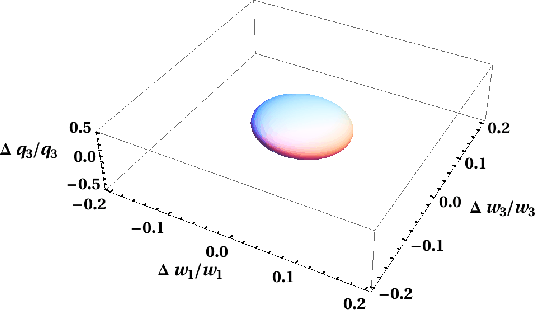
To better visualize the variational effect from the change in the three parameters in both cases, we follow the approach of Osypov et al. (2008), compute the quadratic form of
![]() and plot its contour at a given amount of change in the exact phase velocity expression,
and plot its contour at a given amount of change in the exact phase velocity expression,
| (66) |
|
|---|
|
thomsenmatrix,zonematrix
Figure 14. Ellipsoids obtained from the quadratic form of |
|
|
|
|
|
|
On anelliptic approximations for qP velocities in TI and orthorhombic media |