Published as IEEE Geoscience and Remote Sensing Letters, 12, no. 10, 2150-2154, (2015)
De-aliased seismic data interpolation using seislet transform with low-frequency constraint
Shuwei Gan , Shoudong Wang
, Shoudong Wang , Yangkang Chen
, Yangkang Chen , Yizhuo Zhang
, Yizhuo Zhang , Zhaoyu Jin
, Zhaoyu Jin
 State Key Laboratory of Petroleum Resources and Prospecting
State Key Laboratory of Petroleum Resources and Prospecting
China University of Petroleum
Fuxue Road 18th
Beijing, China, 102200
gsw19900128@126.com
 Jackson School of Geosciences
Jackson School of Geosciences
The University of Texas at Austin
University Station, Box X
Austin, TX 78713-8924, USA
Email: ykchen@utexas.edu
 Institut de Physique du Globe de Paris (IPGP)
Institut de Physique du Globe de Paris (IPGP)
1 Rue Jussieu
75005 Paris, France
Email: yizhuozh@gmail.com
 School of Geosciences,
University of Edinburgh,
Edinburgh,UK, EH9 3JW,
Email: s1263999@sms.ed.ac.uk
School of Geosciences,
University of Edinburgh,
Edinburgh,UK, EH9 3JW,
Email: s1263999@sms.ed.ac.uk
Abstract:
Interpolating regularly missing traces in seismic data is thought to be much harder than interpolating irregularly missing seismic traces, because many sparsity-based approaches can not be used due to the strong aliasing noise in the sparse domain. We propose to use seislet transform to perform a sparsity-based approach to interpolate highly under-sampled seismic data based on the classic projection onto convex sets (POCS) framework. Many numerical tests show that the local slope is the main factor that will affect the sparsity and anti-aliasing ability of seislet transform. By low-pass filtering the under-sampled seismic data with a very low bound frequency, we can get a precise dip estimation, which will make seislet transform capable for interpolating the aliased seismic data. In order to prepare the optimum local slope during iterations, we update the slope field every several iterations. We also use a percentile thresholding approach to better control the reconstruction performance. Both synthetic and field examples show better performance using the proposed approach than the traditional prediction based and the
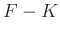
POCS based approaches.
2020-02-21
![]() , Shoudong Wang
, Shoudong Wang![]() , Yangkang Chen
, Yangkang Chen![]() , Yizhuo Zhang
, Yizhuo Zhang![]() , Zhaoyu Jin
, Zhaoyu Jin![]()
![]() State Key Laboratory of Petroleum Resources and Prospecting
State Key Laboratory of Petroleum Resources and Prospecting
![]() Jackson School of Geosciences
Jackson School of Geosciences
![]() Institut de Physique du Globe de Paris (IPGP)
Institut de Physique du Globe de Paris (IPGP)
![]() School of Geosciences,
University of Edinburgh,
Edinburgh,UK, EH9 3JW,
Email: s1263999@sms.ed.ac.uk
School of Geosciences,
University of Edinburgh,
Edinburgh,UK, EH9 3JW,
Email: s1263999@sms.ed.ac.uk