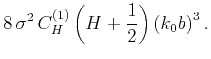|
 |
 |
 | Fractal heterogeneities in sonic logs
and low-frequency scattering attenuation |  |
![[pdf]](icons/pdf.png) |
Next: Penetration depth
Up: Scattering attenuation in 3D
Previous: Low-frequency waves in 3D
The energy spectrum,
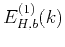 , of von Kármán's autocorrelation
function
, of von Kármán's autocorrelation
function 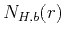 in equation 7 is real and even:
in equation 7 is real and even:
Values of 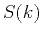 defined by equation 22 are
defined by equation 22 are
Coefficient 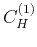 , defined by equation 8, is an increasing function of exponent
, defined by equation 8, is an increasing function of exponent 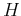 and has to be calculated numerically, except for some specific values:
and has to be calculated numerically, except for some specific values:
The dispersion relation of equation 21 solves for an explicit solution of attenuation and dispersion:
When 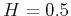 , the derivation produces simple expressions as detailed in Appendix B.
The use of
, the derivation produces simple expressions as detailed in Appendix B.
The use of
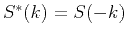 with the Kramers-Krönig relation can be used
to determine the real part of
with the Kramers-Krönig relation can be used
to determine the real part of 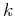 .
In the context of the second-order approximation,
scattering attenuation in a von Kármán isotropic medium is
.
In the context of the second-order approximation,
scattering attenuation in a von Kármán isotropic medium is
![$\displaystyle \frac{1}{Q} = \frac{2\,Im[k]}{Re[k]} = 2~\sigma^2\,k_0b~C^{(1)}_{H}
\left[1-\frac{1}{(1+4\,b^2k_0^2)^{H+\frac{1}{2}}}\right].$](img192.png) |
|
|
(31) |
For 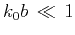 , the scattering attenuation reduces to the Rayleigh diffusion regime:
, the scattering attenuation reduces to the Rayleigh diffusion regime:
Subsections
 |
 |
 |
 | Fractal heterogeneities in sonic logs
and low-frequency scattering attenuation |  |
![[pdf]](icons/pdf.png) |
Next: Penetration depth
Up: Scattering attenuation in 3D
Previous: Low-frequency waves in 3D
2013-07-26
![]() , of von Kármán's autocorrelation
function
, of von Kármán's autocorrelation
function ![]() in equation 7 is real and even:
in equation 7 is real and even:
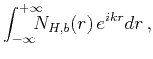

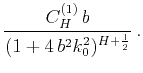
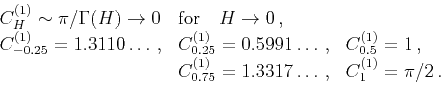
![$\displaystyle 1+\frac{\sigma^2}{2}\left(1+2k_0~Im[S(2k_0)]\right)\,,$](img187.png)
![$\displaystyle \sigma^2k_0b~C^{(1)}_{H}
\left[1-\frac{1}{(1+4\,b^2k_0^2)^{H+\frac{1}{2}}} \right].$](img189.png)
![$\displaystyle \frac{1}{Q} = \frac{2\,Im[k]}{Re[k]} = 2~\sigma^2\,k_0b~C^{(1)}_{H}
\left[1-\frac{1}{(1+4\,b^2k_0^2)^{H+\frac{1}{2}}}\right].$](img192.png)