 |
 |
 |
 | Least-squares diffraction imaging using shaping regularization by anisotropic smoothing |  |
![[pdf]](icons/pdf.png) |
Next: Determination of edge diffraction
Up: Method
Previous: Method
To solve for a seismic diffraction image
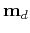 , we extend the approach developed by Merzlikin and Fomel (2016) to three dimensions:
, we extend the approach developed by Merzlikin and Fomel (2016) to three dimensions:
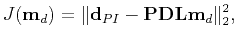 |
(1) |
where
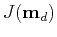 is the objective function,
is the objective function,
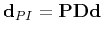 and
and
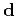 is ``observed'' data.
Here, forward modeling corresponds to the chain of operators: three-dimensional path-summation integral filter
is ``observed'' data.
Here, forward modeling corresponds to the chain of operators: three-dimensional path-summation integral filter
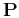 (Merzlikin and Fomel, 2015,2017),
azimuthal plane wave destruction (AzPWD) filter
(Merzlikin and Fomel, 2015,2017),
azimuthal plane wave destruction (AzPWD) filter
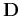 (Merzlikin et al., 2017b,2016) and three-dimensional Kirchhoff modeling
(Merzlikin et al., 2017b,2016) and three-dimensional Kirchhoff modeling
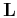 .
The path-summation integral filter
.
The path-summation integral filter
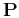 can be treated as the probability
of a diffraction at a certain location. Azimuthal plane wave destruction filter
can be treated as the probability
of a diffraction at a certain location. Azimuthal plane wave destruction filter
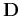 removes reflected energy perpendicular to the edges.
Therefore, AzPWD
emphasizes edge diffraction signature, which when measured in the direction perpendicular to the edge
exhibits a hyperbolic moveout and kinematically behaves as a reflection when observed along the edge.
AzPWD application is the key distinction from the 2D version of the workflow (Merzlikin and Fomel, 2016), in which
plane-wave destruction filter (PWD) (Fomel, 2002) is applied along the time-distance
plane (Fomel et al., 2007; Merzlikin et al., 2018).
After weighting the data
removes reflected energy perpendicular to the edges.
Therefore, AzPWD
emphasizes edge diffraction signature, which when measured in the direction perpendicular to the edge
exhibits a hyperbolic moveout and kinematically behaves as a reflection when observed along the edge.
AzPWD application is the key distinction from the 2D version of the workflow (Merzlikin and Fomel, 2016), in which
plane-wave destruction filter (PWD) (Fomel, 2002) is applied along the time-distance
plane (Fomel et al., 2007; Merzlikin et al., 2018).
After weighting the data
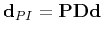 by path-summation integral
by path-summation integral
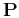 and AzPWD filter
and AzPWD filter
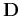 , model fitting is constrained to most probable diffraction locations.
, model fitting is constrained to most probable diffraction locations.
 |
 |
 |
 | Least-squares diffraction imaging using shaping regularization by anisotropic smoothing |  |
![[pdf]](icons/pdf.png) |
Next: Determination of edge diffraction
Up: Method
Previous: Method
2021-02-24
![]() , we extend the approach developed by Merzlikin and Fomel (2016) to three dimensions:
, we extend the approach developed by Merzlikin and Fomel (2016) to three dimensions: