|
|
|
|
Multidimensional recursive filter preconditioning in geophysical estimation problems |

|
|---|
|
data
Figure 1. The input data (right) are irregularly spaced samples of a sinusoid (left). |
|
|
In the first example, the input data ![]() were randomly
subsampled (with decreasing density) from a sinusoid (Figure
1). The forward operator
were randomly
subsampled (with decreasing density) from a sinusoid (Figure
1). The forward operator ![]() in this case is
linear interpolation. In other words, we seek a regularly sampled
model
in this case is
linear interpolation. In other words, we seek a regularly sampled
model ![]() on 200 grid points that could predict the data with a
forward linear interpolation. Sparse irregular distribution of the
input data makes the regularization necessary. We applied convolution
with the simple
on 200 grid points that could predict the data with a
forward linear interpolation. Sparse irregular distribution of the
input data makes the regularization necessary. We applied convolution
with the simple ![]() difference filter as the operator
difference filter as the operator ![]() that forces model continuity (the first-order spline). An appropriate
preconditioner
that forces model continuity (the first-order spline). An appropriate
preconditioner ![]() in this case is the inverse of
in this case is the inverse of ![]() ,
which amounts to recursive causal integration (Claerbout, 1999). Figures
2 and 3 show the results of inverse
interpolation after exhaustive 300 iterations of the
conjugate-direction method. The results from the model-space and
data-space regularization look similar except for the boundary
conditions outside the data range. As a result of using the causal
integration for preconditioning, the rightmost part of the model in
the data-space case stays at a constant level instead of decreasing to
zero. If we specifically wanted a zero-value boundary condition, we
could easily implement it by adding a zero-value data point at the
boundary.
,
which amounts to recursive causal integration (Claerbout, 1999). Figures
2 and 3 show the results of inverse
interpolation after exhaustive 300 iterations of the
conjugate-direction method. The results from the model-space and
data-space regularization look similar except for the boundary
conditions outside the data range. As a result of using the causal
integration for preconditioning, the rightmost part of the model in
the data-space case stays at a constant level instead of decreasing to
zero. If we specifically wanted a zero-value boundary condition, we
could easily implement it by adding a zero-value data point at the
boundary.

|
|---|
|
im1
Figure 2. Estimation of a continuous function by the model-space regularization. The difference operator |
|
|

|
|---|
|
fm1
Figure 3. Estimation of a continuous function by the data-space regularization. The preconditioning operator |
|
|
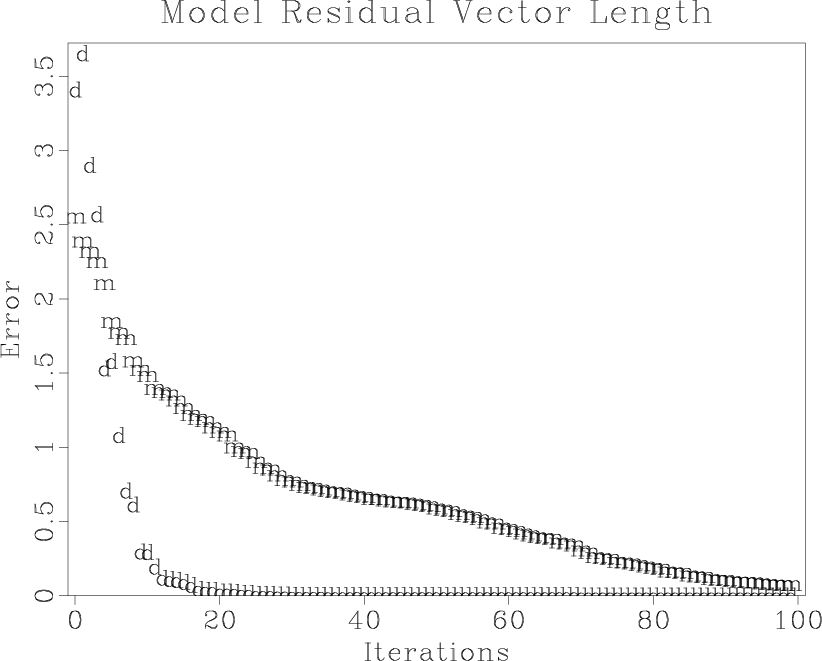
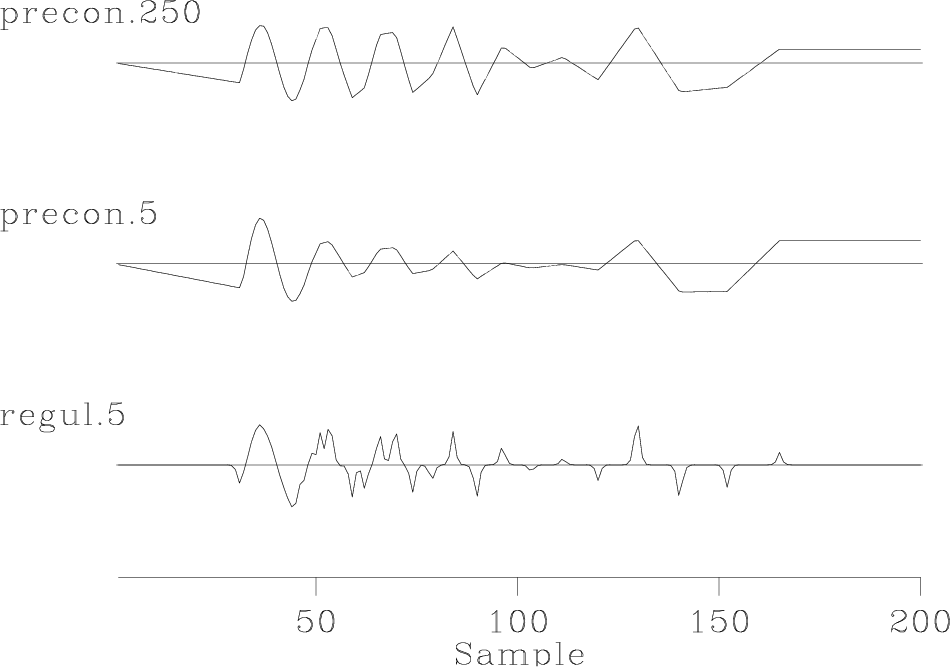
The model preconditioning approach provides a much faster rate of convergence. We measured the rate of convergence using the power of the model residual, defined as the least-squares distance from the current model to the final solution. Figure 4 shows that the preconditioning (data regularization) method converged to the final solution in about 6 times fewer iterations than the model regularization. Since the cost of each iteration for both methods is roughly equal, the computational economy is evident. Figure 5 shows the final solution, and the estimates from model- and data-space regularization after only 5 iterations of conjugate directions. The data-space estimate appears much closer to the final solution.
|
|---|
|
schwab1
Figure 4. Convergence of the iterative optimization, measured in terms of the model residual. The ``d'' points stand for data-space regularization; the ``m'' points for model-space regularization. |
|
|
|
|---|
|
early1
Figure 5. The top figure is the exact solution found in 250 iterations. The middle is with data-space regularization after 5 iterations. The bottom is with model-space regularization after 5 iterations. |
|
|
Changing the preconditioning operator changes the regularization
result. Figure 6 shows the result of data-space
regularization after a triangle smoother is applied as the model
preconditioner. Triangle smoother is a filter with the ![]() -transform
-transform
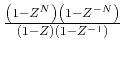 (Claerbout, 1992). We chose the filter length
(Claerbout, 1992). We chose the filter length ![]() .
.
|
fm6
Figure 6. Estimation of a smooth function by the data-space regularization. The preconditioning operator |
|
|---|---|
|
|
If, instead of looking for a smooth interpolation, we want to limit the number
of frequency components, then the optimal choice for the model-space
regularization operator ![]() is a prediction-error filter (PEF). To
obtain a mono-frequency output, we can use a three-point PEF, which has the
is a prediction-error filter (PEF). To
obtain a mono-frequency output, we can use a three-point PEF, which has the
![]() -transform representation
-transform representation
![]() . In this case, the
corresponding preconditioner
. In this case, the
corresponding preconditioner ![]() can be the three-point
recursive filter
can be the three-point
recursive filter
![]() . To test this
idea, we estimated the PEF
. To test this
idea, we estimated the PEF ![]() from the output of inverse linear
interpolation (Figure 3), and ran the data-space regularized
estimation again, substituting the recursive filter
from the output of inverse linear
interpolation (Figure 3), and ran the data-space regularized
estimation again, substituting the recursive filter
![]() in place
of the causal integration. We repeated this two-step procedure three times to
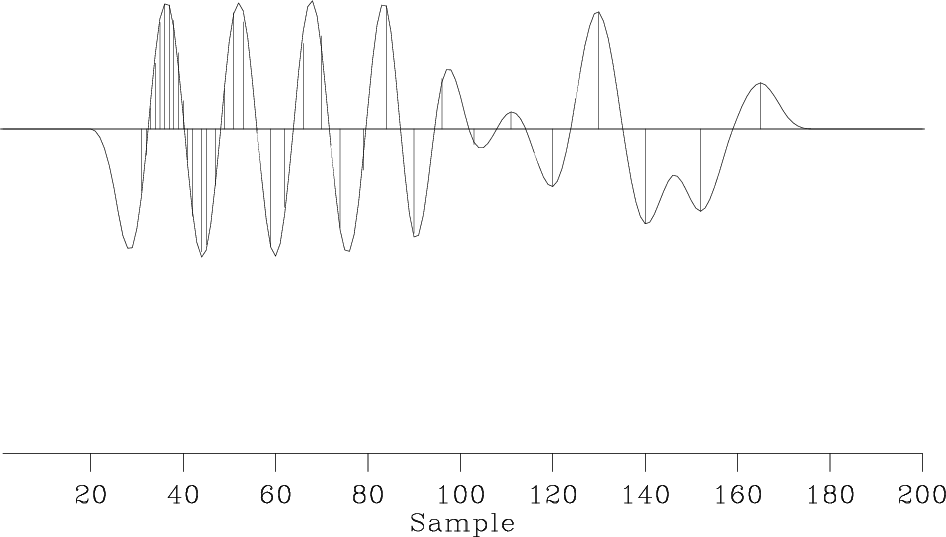
get a better estimate for the PEF. The result, shown in Figure 7,
exhibits the desired mono-frequency output. One can accommodate more frequency
components in the model using a longer filter.
in place
of the causal integration. We repeated this two-step procedure three times to
get a better estimate for the PEF. The result, shown in Figure 7,
exhibits the desired mono-frequency output. One can accommodate more frequency
components in the model using a longer filter.
|
pm1
Figure 7. Estimation of a mono-frequency function by the data-space regularization. The preconditioning operator |

|
|---|---|
|
|
|
|
|
|
Multidimensional recursive filter preconditioning in geophysical estimation problems |