 |
 |
 |
 | Amplitude preservation for offset continuation:
Confirmation for Kirchhoff data |  |
![[pdf]](icons/pdf.png) |
Next: DISCUSSION
Up: Fomel & Bleistein: Offset
Previous: THE KIRCHHOFF MODELING APPROXIMATION
In this section, we introduce the offset continuation partial
differential equation. We then develop its WKBJ, or ray theoretic,
solution for phase and leading-order amplitude. We explain how we
verify that the traveltime and amplitude of the integrand of the
Kirchhoff representation (4) satisfy the ``eikonal'' and
``transport'' equations of the OC partial differential equation. To
do so, we make use of relationship (15), derived from
the Kirchhoff integral.
The offset continuation differential
equation derived in earlier papers
(Fomel, 2003,1994)![[*]](icons/footnote.png) is
is
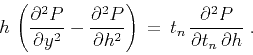 |
(16) |
In this equation, 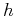 is the half-offset (
is the half-offset (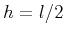 ),
), 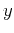 is the midpoint
(
is the midpoint
(
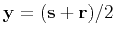 ) [hence,
) [hence, 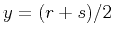 ],
and
],
and  is the NMO-corrected traveltime
is the NMO-corrected traveltime
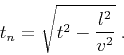 |
(17) |
Equation (16) describes the process of
seismogram transformation in the time-midpoint-offset domain. One can
obtain the high-frequency asymptotics of its solution by standard
methods, as follows.
We introduce a trial asymptotic solution of the form
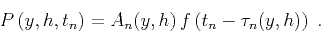 |
(18) |
It is important to remember the assumption that 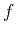 is a
``rapidly varying function,'' for example, a bandlimited delta
function.
We substitute this solution
into equation (16) and collect the terms
in order of derivatives of
is a
``rapidly varying function,'' for example, a bandlimited delta
function.
We substitute this solution
into equation (16) and collect the terms
in order of derivatives of 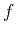 .
This is the direct counterpart of collecting terms in powers of
frequency when applying WKBJ in the frequency domain.
From the leading
asymptotic order (the second derivative of the function
.
This is the direct counterpart of collecting terms in powers of
frequency when applying WKBJ in the frequency domain.
From the leading
asymptotic order (the second derivative of the function 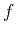 ), we
obtain the eikonal equation describing the kinematics of the OC
transformation:
), we
obtain the eikonal equation describing the kinematics of the OC
transformation:
![\begin{displaymath}
h \left[ {\left( \partial \tau_n \over \partial y \right)...
...t] = - \tau_n {\partial \tau_n \over \partial h} \;.
\end{displaymath}](img57.png) |
(19) |
In this equation, we have replaced a multiplier of  by
by
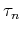 on the right side of the equation. This is consistent with
our assumption that
on the right side of the equation. This is consistent with
our assumption that 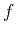 is a bandlimited delta function or some
equivalent impulsive source.
Analogously, collecting the terms containing the first derivative of
is a bandlimited delta function or some
equivalent impulsive source.
Analogously, collecting the terms containing the first derivative of
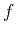 leads to the transport equation describing the transformation
of the amplitudes:
leads to the transport equation describing the transformation
of the amplitudes:
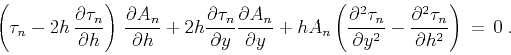 |
(20) |
We then rewrite the eikonal equation (19) in the
time-source-receiver coordinate system, as follows:
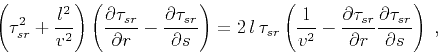 |
(21) |
which makes it easy (using Mathematica) to verify that the explicit
expression for the phase of the Kirchhoff integral kernel (6)
satisfies the eikonal equation for any scattering point![[*]](icons/footnote.png)
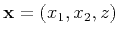 . Here,
. Here,  is related to
is related to 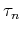 as
as 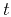 is related
to
is related
to  in equation (17).
in equation (17).
The general solution of the amplitude equation (20)
has the form (Fomel, 2003)
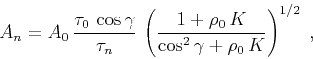 |
(22) |
where 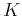 is the reflector curvature at the reflection point. The
kernel (5) of the Kirchhoff integral (4)
corresponds to the reflection from a point diffractor: the integral
realizes the superposition of Huygens secondary source contributions.
We can obtain the solution of the amplitude equation for this case by
formally setting the curvature
is the reflector curvature at the reflection point. The
kernel (5) of the Kirchhoff integral (4)
corresponds to the reflection from a point diffractor: the integral
realizes the superposition of Huygens secondary source contributions.
We can obtain the solution of the amplitude equation for this case by
formally setting the curvature 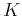 to infinity (setting the radius of
curvature to zero). The infinite curvature transforms formula
(22) to the relationship
to infinity (setting the radius of
curvature to zero). The infinite curvature transforms formula
(22) to the relationship
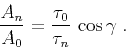 |
(23) |
Again, we exploit the assumption that
the signal 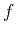 has the form of the delta function.
In this case, the amplitudes
before and after the NMO correction are connected according to the
known properties of the delta function, as follows:
has the form of the delta function.
In this case, the amplitudes
before and after the NMO correction are connected according to the
known properties of the delta function, as follows:
 |
(24) |
with
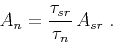 |
(25) |
Combining equations (25) and (23) yields
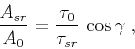 |
(26) |
which coincides exactly with the previously found formula
(15). As with the solution of the eikonal equation, we pass
from an in-plane solution in two dimensions to a solution for a
scattering point in three dimensions by replacing 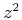 with
with 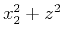 .
.
Although the presented equations pertain to the case of offset
continuation that starts from 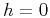 , i.e., inverse DMO, this is
sufficient, since every other continuation can be obtained as a chain
of DMO and inverse DMO.
, i.e., inverse DMO, this is
sufficient, since every other continuation can be obtained as a chain
of DMO and inverse DMO.
Thus, it is apparent that the OC differential equation
(16) relates to the Kirchhoff representation of
reflection data. We see that the amplitude and phase of the Kirchhoff
representation for arbitrary offset is the point diffractor WKBJ
solution of the offset continuation differential equation. Hence, the
Kirchhoff approximation is a solution of the OC differential equation
when we hold the reflection coefficient constant. This means that the
solution of the OC differential equation has all the features of
amplitude preservation, as does the Kirchhoff representation,
including geometrical spreading, curvature effects, and phase shift
effects. Furthermore, in the Kirchhoff representation and the
solution of the OC partial differential equation by WKBJ, we have not
used the 2.5-D assumption. Therefore the preservation of amplitude is
not restricted to cylindrical surfaces as it is in the true-amplitude
proof for DMO (Bleistein et al., 2001). This is what we sought to confirm.
 |
 |
 |
 | Amplitude preservation for offset continuation:
Confirmation for Kirchhoff data |  |
![[pdf]](icons/pdf.png) |
Next: DISCUSSION
Up: Fomel & Bleistein: Offset
Previous: THE KIRCHHOFF MODELING APPROXIMATION
2013-03-03
![]() is
is
![]() has the form of the delta function.
In this case, the amplitudes
before and after the NMO correction are connected according to the
known properties of the delta function, as follows:
has the form of the delta function.
In this case, the amplitudes
before and after the NMO correction are connected according to the
known properties of the delta function, as follows:
![]() , i.e., inverse DMO, this is
sufficient, since every other continuation can be obtained as a chain
of DMO and inverse DMO.
, i.e., inverse DMO, this is
sufficient, since every other continuation can be obtained as a chain
of DMO and inverse DMO.