 |
 |
 |
 | Effective AMO implementation in the log-stretch,
frequency-wavenumber domain |  |
![[pdf]](icons/pdf.png) |
Next: F-K filtering
Up: Vlad and Biondi: Log-stretch
Previous: The log-stretch, frequency-wavenumber AMO
For the purpose of this discussion we define stretching of a
single-dimension space as any transformation from one space to
another that has the following property: at least an arbitrarily chosen sequence
of two consecutive, equal in length, intervals in the input space is
transformed into a sequence of two consecutive,  equal in length,
intervals in the output space. Stretching an x-space to a y-space will be denoted as
equal in length,
intervals in the output space. Stretching an x-space to a y-space will be denoted as
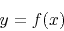 |
(6) |
Two obvious examples of stretching are
where 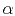 is a positive real number whose value does not matter
for the purpose of this discussion. As it can be seen in
Fig. 2, if we keep the same sampling rate (
is a positive real number whose value does not matter
for the purpose of this discussion. As it can be seen in
Fig. 2, if we keep the same sampling rate (
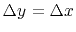 ), aliasing can occur when doing the reverse transformation,
from x to y. In order to avoid aliasing, we need to compute
), aliasing can occur when doing the reverse transformation,
from x to y. In order to avoid aliasing, we need to compute
 , the largest accceptable sampling rate in the y
domain. This can sometimes lead to a larger number of samples in the
, the largest accceptable sampling rate in the y
domain. This can sometimes lead to a larger number of samples in the
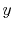 domain, and thus to larger computational expense. This can be
limited to some extent if the signal in the
domain, and thus to larger computational expense. This can be
limited to some extent if the signal in the 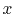 -space has been
bandpassed, as is often the case with seismic data, with the largest
frequency present in the data (
-space has been
bandpassed, as is often the case with seismic data, with the largest
frequency present in the data (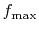 ) smaller than the Nyquist
frequency given by the sampling rate (
) smaller than the Nyquist
frequency given by the sampling rate (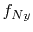 ). Thus, we can replace in our calculations
). Thus, we can replace in our calculations 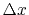 with
with
which will result in a
 larger than that computed using
larger than that computed using 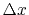 , the sampling rate in the
, the sampling rate in the 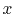 space.
space.
|
|---|
strali
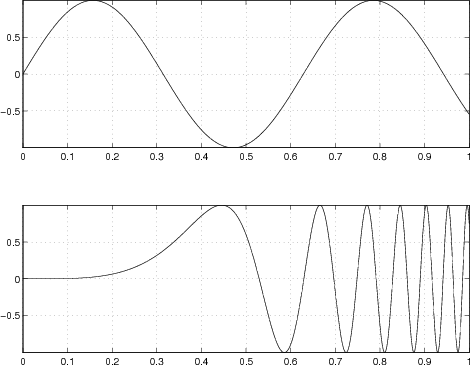
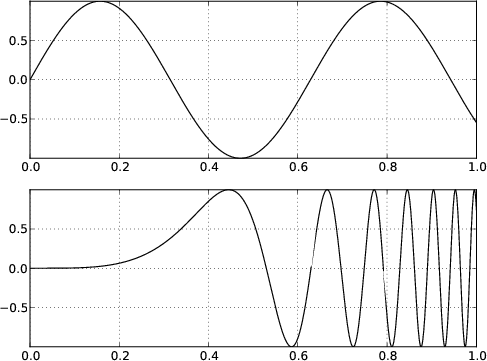
Figure 2. Illustration of how aliasing can occur
while stretching: if the same sampling rate is used for the 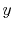 -space
(lower plot) as for the -space
(lower plot) as for the 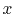 -space (upper plot), serious aliasing will
occur when transforming back to -space (upper plot), serious aliasing will
occur when transforming back to 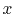 -space. This will not happen if the
sampling rate in the -space. This will not happen if the
sampling rate in the 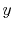 -space is smaller than or equal to -space is smaller than or equal to

|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[matlab]](icons/matlab.png)
|
|---|
|
|---|
pystrali
Figure 3. Illustration of how aliasing can occur
while stretching: if the same sampling rate is used for the 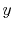 -space
(lower plot) as for the -space
(lower plot) as for the 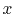 -space (upper plot), serious aliasing will
occur when transforming back to -space (upper plot), serious aliasing will
occur when transforming back to 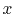 -space. This will not happen if the
sampling rate in the -space. This will not happen if the
sampling rate in the 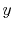 -space is smaller than or equal to -space is smaller than or equal to

|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[pylab]](icons/pylab.png)
|
|---|
In order to compute
 , we will consider two points in the
, we will consider two points in the 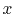 space, as seen in Fig. 2, such as
space, as seen in Fig. 2, such as
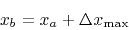 |
(7) |
and 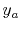 and
and 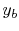 , the images of
, the images of 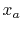 and
and 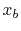 in the
in the 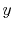 space. Thus,
space. Thus,
The largest sampling rate in the 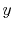 -space that will not result in aliasing is
-space that will not result in aliasing is
 , the minimum possible value of
, the minimum possible value of 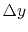 . Suppose there is a value
. Suppose there is a value 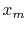 that minimizes
that minimizes 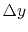 . Then,
. Then,
In particular, in the case of log-stretch, given by equation (1), if 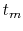 plays the role of
plays the role of 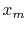 from the equation above, then
from the equation above, then
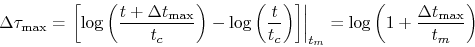 |
(8) |
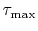 will be minimum when
will be minimum when 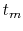 is as large as possible,
thus minimizing the expression under the logarithm. How large can
is as large as possible,
thus minimizing the expression under the logarithm. How large can 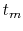 get? Since the length of the seismic trace is limited to a value
get? Since the length of the seismic trace is limited to a value 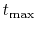 ,
,
because 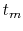 is the equivalent of
is the equivalent of 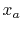 from eq. (7) and Fig. 2. Thus, we get
from eq. (7) and Fig. 2. Thus, we get
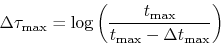 |
(9) |
 |
 |
 |
 | Effective AMO implementation in the log-stretch,
frequency-wavenumber domain |  |
![[pdf]](icons/pdf.png) |
Next: F-K filtering
Up: Vlad and Biondi: Log-stretch
Previous: The log-stretch, frequency-wavenumber AMO
2013-03-03
![]() equal in length,
intervals in the output space. Stretching an x-space to a y-space will be denoted as
equal in length,
intervals in the output space. Stretching an x-space to a y-space will be denoted as
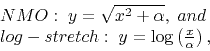


![]() , we will consider two points in the
, we will consider two points in the ![]() space, as seen in Fig. 2, such as
space, as seen in Fig. 2, such as