|
|
|
|
Imaging complex structures with first-arrival traveltimes |
Green's functions based on first-arrival traveltime calculation methods result in poor images in structurally complex areas. Several reasons have been given for this failure:
Complexity of velocity models and validity of high-frequency approximations can be defined in various ways. The larger the velocity model, the more variation there will tend to be and the more opportunity there will be for things to go wrong: There will be more opportunity for frequency components to separate, for headwaves to develop, and for triplications to occur.

|
|---|
|
velfig
Figure 1. The Marmousi velocity model. |
|
|
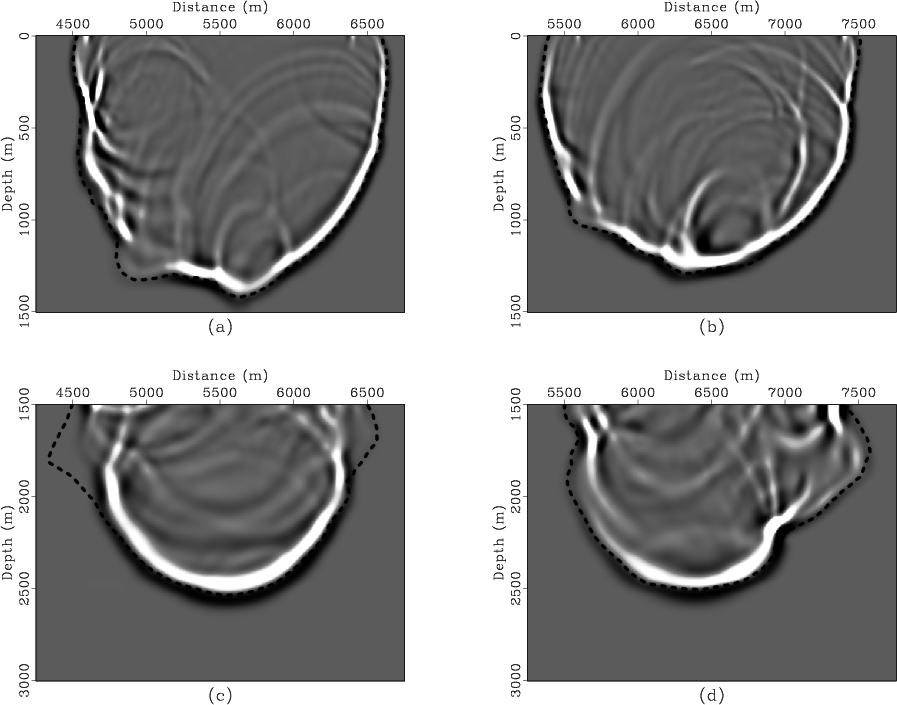
The Marmousi velocity model (Figure 1) results in complex propagation paths where late energetic arrivals are not fit well by first-arrival finite-difference traveltimes. In Figure 2, an acoustic modeling program was used to generate snapshots of the wavefield from two surface source locations in the Marmousi model. The corresponding contours of finite-difference traveltime at 1.05 s have been overlain. Clearly, the finite-difference traveltime contours do not always correspond to energetic portions of the wavefield. If these traveltimes were used for migration, the resulting image would suffer because parts of the summation trajectories would not correspond to energetic arrivals. By contrast, snapshots for the same source locations at an earlier time of 0.6 s (Figures 3a and 3b) show that the finite-difference traveltime curves overlay the high energy portions of the wavefields nicely. This is because there has not been enough time for adverse propagation effects to fully develop. Figures 3c and 3d are generated by starting the acoustic modeling and the finite-difference traveltime calculation from a depth of 1500 m. The 0.3 s contours correspond nicely to the high energy portions of the wavefields. There is some deviation in the shallow part of Figure 3c, but for the most part the finite-difference traveltime contour fits the bulk of the acoustic energy pretty well. Overall, the contours in Figure 3 have not pulled away from the wavefield as they have in Figure 2.

|
|---|
|
snap0
Figure 2. The result of acoustic wavefield modeling for the Marmousi model overlain by contours of finite-difference traveltime. Snapshots (a) and (b) are taken at a time of 1.05 s for two different source locations. |
|
|
|
|---|
|
snapdatum
Figure 3. The result of acoustic wavefield modeling for the Marmousi model overlain by contours of finite-difference traveltime. Snapshots (a) and (b) are taken at a time of 0.6 s for the same two source locations depicted in Figure 2. Snapshots (c) and (d) are taken at a time of 0.3 s with sources at a depth of 1500 m and the same lateral positions as in (a) and (b). |
|
|
These properties of first-arrival traveltimes, and the observation that Kirchhoff migration using first-arrival traveltimes usually produces an acceptable image of the upper 1500 m of the Marmousi synthetic, motivated the development of the layer-striping method described here.
Throughout this study, I use a finite difference solution to the eikonal equation to generate traveltimes (van Trier and Symes, 1991). I use my Kirchhoff datuming algorithm (Bevc, 1993), and an industry standard Kirchhoff migration code to generate the results.
|
|
|
|
Imaging complex structures with first-arrival traveltimes |