The double-elliptic approximation in the group and phase domains

Conclusions

The double-elliptic approximation introduced by Muir (1990) can approximate the kinematics of TI media quite accurately, although it is forced to cut off triplications when fit in the impulse-response domain. In the dispersion-relation domain it remains accurate even for triplicating media.

Our analysis in this paper was limited to simple kinematics. Before pronouncing the double-elliptic approximation a success, we need to also demonstrate how it works when used as the basis for an imaging technique; i.e, how accurately does it model the dynamics of the wave equation? Karrenbach (1991) examines this question in a companion paper.

compare
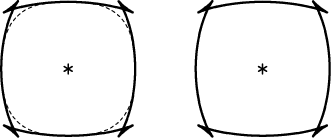
Figure 4. Two different double-elliptic approximations (dashed curves) fit to the qSV mode of Greenhorn Shale (solid curves). Left: the approximation is fit in the impulse-response domain, and so the dashed curve has a simple analytic form. Right: the approximation is fit in the dispersion-relation domain, and so is able to closely follow the triplication. This approximating curve can only be calculated parametrically, however, and so is less useful.

compare2
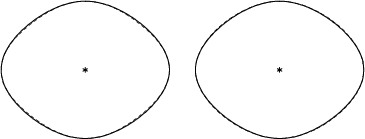
Figure 5. Two different double-elliptic approximations (dashed curves) corresponding to those in Figure 4, but this time fit to the qP mode of Greenhorn Shale (solid curves). (The size of the ``$*$'' in the middle shows the relative scales.) The discrepancy is much less since there are no troublesome triplications.

The double-elliptic approximation in the group and phase domains