|
|
|
|
Least-square inversion with inexact adjoints. Method of conjugate directions: A tutorial |
We are looking for the solution of the linear operator equation
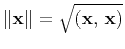 denotes the norm of
denotes the norm of
|
dirres
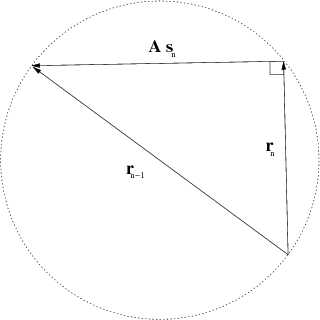
Figure 1. Geometry of the residual in the data space (a scheme). |
|
|---|---|
|
|
|
|
|
|
Least-square inversion with inexact adjoints. Method of conjugate directions: A tutorial |