|
|
|
|
Least-square inversion with inexact adjoints. Method of conjugate directions: A tutorial |
Matthias Schwab has suggested (in a personal communication) an
interesting example, in which the cgstep program fails to
comply with the conjugate-gradient theory. The inverse problem is a
simple one-dimensional data interpolation with a known filter
(, ). The known portion of the data is a single
spike in the middle. One hundred other data points are considered
missing. The known filter is the Laplacian ![]() , and the
expected result is a bell-shaped cubic spline. The forward problem is
strictly linear, and the exact adjoint is easily computed by reverse
convolution. However, the conjugate-gradient program requires
significantly more than the theoretically predicted 100
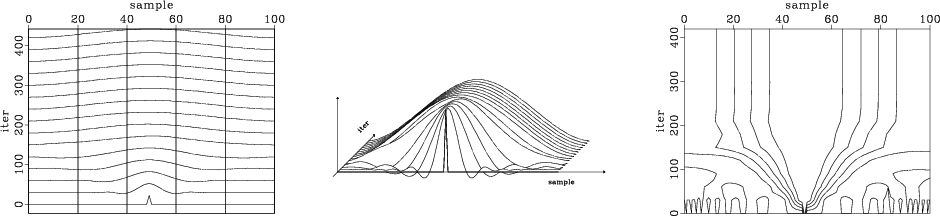
iterations. Figure 2 displays the convergence to the
final solution in three different plots. According to the figure, the
actual number of iterations required for convergence is about
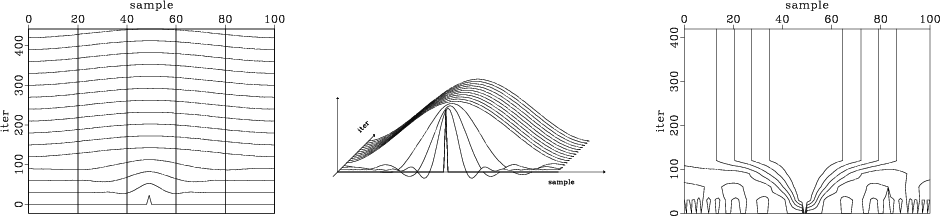
300. Figure 3 shows the result of a similar experiment
with the conjugate-direction solver
, and the
expected result is a bell-shaped cubic spline. The forward problem is
strictly linear, and the exact adjoint is easily computed by reverse
convolution. However, the conjugate-gradient program requires
significantly more than the theoretically predicted 100
iterations. Figure 2 displays the convergence to the
final solution in three different plots. According to the figure, the
actual number of iterations required for convergence is about
300. Figure 3 shows the result of a similar experiment
with the conjugate-direction solver cdstep. The number of
required iterations is reduced to almost the theoretical one
hundred. This indicates that the orthogonality of directions implied
in the conjugate-gradient method has been distorted by computational
errors. The additional cost of correcting these errors with the
conjugate-direction solver comes from storing the preceding 100
directions in memory. A smaller number of memorized steps produces
smaller improvements.
|
|---|
|
dirmcg
Figure 2. Convergence of the missing data interpolation problem with the conjugate-gradient solver. Current models are plotted against the number of iterations. The three plots are different displays of the same data. |
|
|
|
|---|
|
dirmcd
Figure 3. Convergence of the missing data interpolation problem with the long-memory conjugate-direction solver. Current models are plotted against the number of iterations. The three plots are different displays of the same data. |
|
|
|
|
|
|
Least-square inversion with inexact adjoints. Method of conjugate directions: A tutorial |