|
|
|
|
Accelerated plane-wave destruction |

|
|---|
|
modl
Figure 2. Harmonic waves with constant slope |
|
|
To test the performance of the proposed slope-estimation method,
we generated a harmonic wave field with constant slope ![]() shown in Figure 2.
We added different scales of additive white Gaussian noise (AWGN)
to the wave field and estimate the slope by the proposed method.
To compare with the iterative algorithm by Fomel (2002),
the mean square error (MSE) is used as the criterion:
shown in Figure 2.
We added different scales of additive white Gaussian noise (AWGN)
to the wave field and estimate the slope by the proposed method.
To compare with the iterative algorithm by Fomel (2002),
the mean square error (MSE) is used as the criterion:
| (22) |
|
|---|
|
mse-fdip,mse-dip
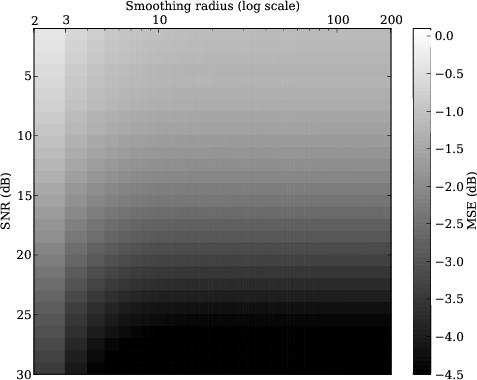
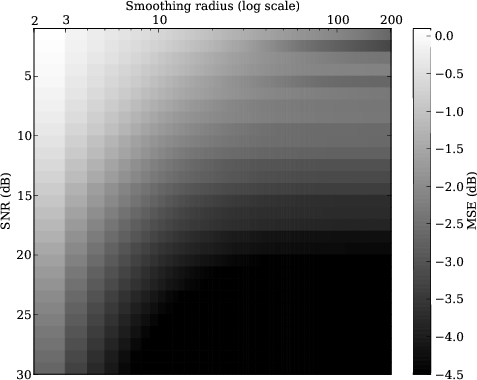
Figure 3. Mean square errors of of the slope estimations by the proposed method (a) and the three-point ( |
|
|
|
|---|
|
runtime
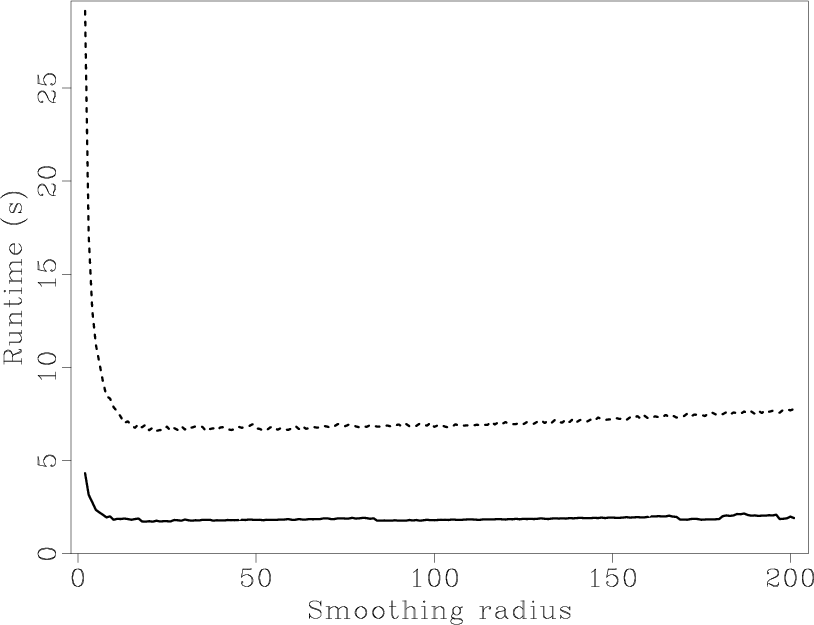
Figure 4. Run time of the proposed method (solid line) and the three-point ( |
|
|
We use five iterations in the iterative method, ![]() .
For constant slope model, using a large smoothing window,
the smoothing regularization can converge faster (with less
.
For constant slope model, using a large smoothing window,
the smoothing regularization can converge faster (with less ![]() )
and we can obtain a better estimation accuracy.
For each methods, we try the smoothing windows from 2 to 200
and show the mean square errors in Figure 3.
Compared with the iterative method,
the proposed method has better accuracy
at the left upper (low SNR and small smoothing window)
and worse accuracy at right bottom corner (high SNR and large smoothing window).
)
and we can obtain a better estimation accuracy.
For each methods, we try the smoothing windows from 2 to 200
and show the mean square errors in Figure 3.
Compared with the iterative method,
the proposed method has better accuracy
at the left upper (low SNR and small smoothing window)
and worse accuracy at right bottom corner (high SNR and large smoothing window).
We show the total runtime of all the noise scale data in Figure 4.
For all smoothing windows in the regularization,
the proposed method (solid line) only uses about one fifth run time
of the three-point (![]() ) iterative method (dash line).
) iterative method (dash line).
A more complicated model
from Claerbout (1999) and Fomel (2002)
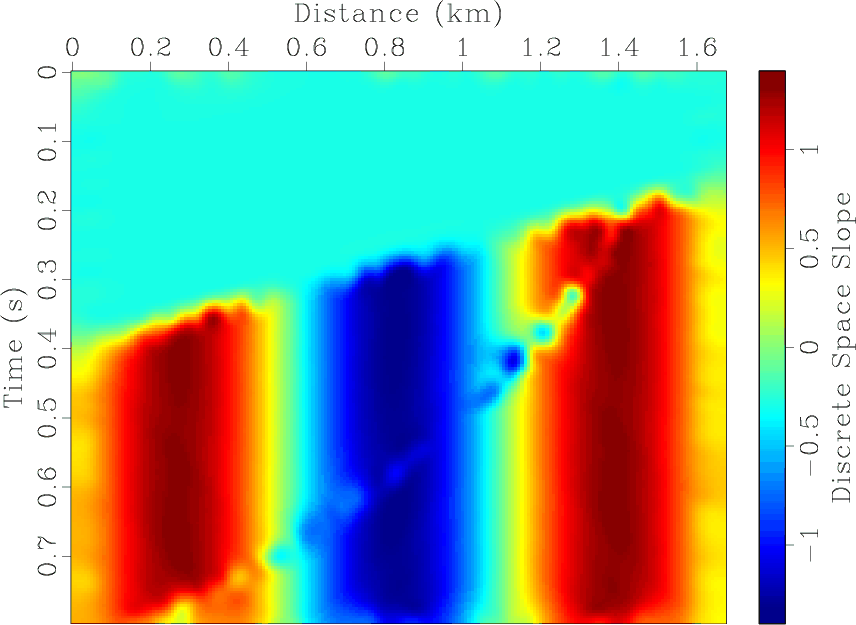
is shown in Figure 5a.
It has variable slopes in synclines, anticlines, and faults.
The slope estimated by the proposed method is shown in
Figure 5b.
The estimation takes about 20 ms.
The three-point (![]() ) iterative method
can obtain a similar estimation (shown in Figure 5c)
by five iterations, which takes about 130ms.
Both methods use a 4-point smoothing window in the regularization,
but the proposed method obtains a slightly smoother estimation.
In Figure 5d we show the faults
detected by the residuals of the proposed plane-wave destruction.
) iterative method
can obtain a similar estimation (shown in Figure 5c)
by five iterations, which takes about 130ms.
Both methods use a 4-point smoothing window in the regularization,
but the proposed method obtains a slightly smoother estimation.
In Figure 5d we show the faults
detected by the residuals of the proposed plane-wave destruction.


|
|---|
|
sigmoid,fdip,dip,pwd-fdip
Figure 5. 2D slope estimation example: (a) synthetic data, (b) slope field estimated by the proposed algorithm, (c) slope field estimated by the iterative algorithm after five iterations, (d) faults detection by plane-wave destruction with the estimated slope. |
|
|
|
|
|
|
Accelerated plane-wave destruction |