 |
 |
 |
 | Signal and noise separation in prestack seismic data using velocity-dependent seislet transform |  |
![[pdf]](icons/pdf.png) |
Next: VD-slope pattern for primary
Up: Theory
Previous: Theory
The seislet transform was introduced by Fomel (2006) and extended by
Fomel and Liu (2010) and Liu and Fomel (2010). The seislet construction is based on
the discrete wavelet transform (DWT) combined with seismic data
patterns, such as local slopes or frequencies. Fomel (2002) developed a
local plane-wave destruction (PWD) operation to predict local
plane-wave events, where an all-pass digital filter is used to
approximate the time shift between two neighboring traces. The inverse
operation, plane-wave construction (Fomel and Guitton, 2006; Fomel, 2010),
predicts a seismic trace from its neighbors by following locally
varying slopes of seismic events and has been used for designing a
PWD-seislet transform, which is a particular kind of the seislet
transforms based on slope patterns. Liu and Liu (2013) proposed a
velocity-dependent (VD) slope as a pattern in VD-seislet transform,
where the normal moveout (NMO) equation serves as a bridge between
local slopes and scanned NMO velocities.
To define seislet transform, we follow the general recipe of the
lifting scheme for the discrete wavelet transform, as described by
Sweldens and Schröder (1996). The construction is reviewed in Appendix A.
Designing pattern-based prediction operator 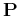 and update
operator
and update
operator 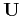 for seismic data is key in the seislet
framework. In the seislet transform, the basic data components can be
different, e.g., traces or common-offset gathers, and the prediction
and update operators shift components according to different patterns.
for seismic data is key in the seislet
framework. In the seislet transform, the basic data components can be
different, e.g., traces or common-offset gathers, and the prediction
and update operators shift components according to different patterns.
The prediction and update operators for a simple seislet transform are
defined by modifying the biorthogonal wavelet construction in
equations from Appendix A as follows:
where 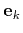 is even components of data at the
is even components of data at the 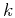 th transform
scale,
th transform
scale, 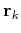 is residual difference between the odd component
of data
is residual difference between the odd component
of data 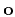 and its prediction from the even component at the
and its prediction from the even component at the
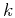 th transform scale, and
th transform scale, and
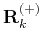 and
and
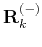 are operators that
predict a component from its left and right neighbors correspondingly
by shifting them according to their patterns. The details are
explained in Appendix A.
are operators that
predict a component from its left and right neighbors correspondingly
by shifting them according to their patterns. The details are
explained in Appendix A.
To get the relationship between prediction operator
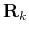 and slope pattern
and slope pattern 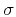 , the plane-wave destruction
operation (Fomel, 2002) can be defined in a linear operator notation as
, the plane-wave destruction
operation (Fomel, 2002) can be defined in a linear operator notation as
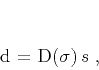 |
(3) |
where seismic section
![$\mathbf{s} = \left[\mathbf{s}_1 \;
\mathbf{s}_2 \; \ldots \; \mathbf{s}_N\right]^T$](img25.png) is a collection of traces, and
is a collection of traces, and
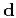 is the destruction residual. The general structure of
is the destruction residual. The general structure of 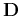 is
defined as follows (Fomel and Guitton, 2006; Fomel, 2010)
is
defined as follows (Fomel and Guitton, 2006; Fomel, 2010)
![\begin{displaymath}
\mathbf{D(\sigma)} =
\left[\begin{array}{ccccc}
\mathbf...
..._{N-1,N}(\sigma_{N-1}) & \mathbf{I} \\
\end{array}\right]\;,
\end{displaymath}](img28.png) |
(4) |
where 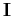 stands for the identity operator,
stands for the identity operator, 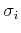 is
local slope pattern, and
is
local slope pattern, and
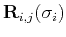 is an operator
for prediction of trace
is an operator
for prediction of trace 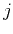 from trace
from trace 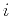 according to the slope
pattern
according to the slope
pattern 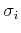 . A trace is predicted by shifting it according to
the local seismic event slopes. Prediction of a trace
from a distant neighbor can be accomplished by simple recursion, i.e.,
predicting trace
. A trace is predicted by shifting it according to
the local seismic event slopes. Prediction of a trace
from a distant neighbor can be accomplished by simple recursion, i.e.,
predicting trace 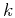 from trace
from trace 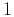 is simply
is simply
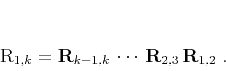 |
(5) |
If 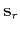 is a reference trace, then the prediction of trace
is a reference trace, then the prediction of trace
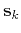 is
is
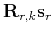 .
.
The predictions need to operate at different scales, which, in this
case, mean different separation distances between the data elements,
e.g., traces in PWD-seislet transform. Equations 1 and
2, in combination with the forward and inverse lifting
schemes, provide a complete definition of the seislet framework. For
different kinds of slope-based seislets, one needs to define the
corresponding slope pattern 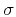 .
.
 |
 |
 |
 | Signal and noise separation in prestack seismic data using velocity-dependent seislet transform |  |
![[pdf]](icons/pdf.png) |
Next: VD-slope pattern for primary
Up: Theory
Previous: Theory
2015-10-24
![]() and update
operator
and update
operator ![]() for seismic data is key in the seislet
framework. In the seislet transform, the basic data components can be
different, e.g., traces or common-offset gathers, and the prediction
and update operators shift components according to different patterns.
for seismic data is key in the seislet
framework. In the seislet transform, the basic data components can be
different, e.g., traces or common-offset gathers, and the prediction
and update operators shift components according to different patterns.
![]() and slope pattern
and slope pattern ![]() , the plane-wave destruction
operation (Fomel, 2002) can be defined in a linear operator notation as
, the plane-wave destruction
operation (Fomel, 2002) can be defined in a linear operator notation as
![]() .
.