 |
 |
 |
 | Conjugate guided gradient (CGG) method for robust inversion and its application to velocity-stack inversion |  |
![[pdf]](icons/pdf.png) |
Next: Examples on synthetic data
Up: Conjugate guided gradient (CGG)
Previous: CGG with residual and
The CGG method described in the previous section can be used to any inversion problem
whose required properties are the robustness to spiky noise and the parsimony of the model.
In this section, the CGG method is tested on a velocity-stack inversion
which is useful not only for velocity analysis
but also for various data processing applications.
The conventional velocity-stack
is performed by summing or estimating semblance Taner and Koehler (1969)
along the various hyperbolas in a CMP gather,
resulting in a velocity-stack panel.
Ideally a hyperbola in a CMP gather should be mapped
onto a point in a velocity-stack panel.
Summation along a hyperbola, or hyperbolic Radon transform (HRT),
does not give such resolution.
To obtain a velocity-stack panel with better resolution,
Thorson and Claerbout (1985) and Hampson (1986)
formulated it as an inverse problem in which the velocity
domain is the unknown space.
If we find an operator  that transforms
a point in a model space (velocity-stack panel)
that transforms
a point in a model space (velocity-stack panel) 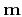 into a hyperbola in data space (CMP gather)
into a hyperbola in data space (CMP gather) 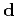 ,
,
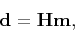 |
(11) |
and also find its adjoint operator  ,
we can pose the velocity-stack problem as an inverse problem.
The adjoint operator
,
we can pose the velocity-stack problem as an inverse problem.
The adjoint operator  corresponds to the velocity stacking operator
for a given range of velocities(or slownesses), which generates a velocity-stack panel
and can be described as
corresponds to the velocity stacking operator
for a given range of velocities(or slownesses), which generates a velocity-stack panel
and can be described as
 |
(12) |
where
 denotes the common-midpoint (CMP) gather and
denotes the common-midpoint (CMP) gather and
 denotes velocity-stack panel.
The slowness-time pair
denotes velocity-stack panel.
The slowness-time pair  are the coordinate axes of the velocity-stack
and the offset-time pair
are the coordinate axes of the velocity-stack
and the offset-time pair  are the coordinate axes of the CMP gather.
A straightforward definition for the forward operator
are the coordinate axes of the CMP gather.
A straightforward definition for the forward operator  is the adjoint
of the operator
is the adjoint
of the operator  defined by Equation (12).
Through the suitable definition of the inner product,
defined by Equation (12).
Through the suitable definition of the inner product,
 turns out to be simply the process of reverse NMO and stacking (Thorson and Claerbout, 1985):
turns out to be simply the process of reverse NMO and stacking (Thorson and Claerbout, 1985):
 |
(13) |
Inverse theory helps us to find an optimal velocity-stack panel which synthesizes
a given CMP gather via the operator  .
The usual process is to implement the inverse as the minimization
of a least-squares problem and calculate the solution by solving
the normal equation:
.
The usual process is to implement the inverse as the minimization
of a least-squares problem and calculate the solution by solving
the normal equation:
 |
(14) |
Since the number of equations and unknowns may be large,
an iterative least-squares solver such as CG is
usually preferred to solving the normal equation directly.
The least-squares solution has some attributes that may be undesirable.
If the model space is overdetermined and has busty noise in data,
the least-squares solutions usually will be spread over all the possible solutions.
Other methods may be more useful
if we desire a parsimonious representation of the solution.
To obtain a more robust solution,
Nichols (1994) and Trad et al. (2003)
used the IRLS method for 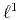 -norm minimization,
and Guiiton and Symes (2003) used
a quasi-Newton method called limited-memory BFGS
Goldfarb (1970); Nocedal (1980); Broyden (1969); Fletcher (1970); Shanno (1970)
for Huber-norm minimization.
Another possibility is the CGG method proposed in the preceding section.
In the next subsections the results of the CGG method
for the velocity-stack inversion are
compared with the results of conventional
LS method and
-norm minimization,
and Guiiton and Symes (2003) used
a quasi-Newton method called limited-memory BFGS
Goldfarb (1970); Nocedal (1980); Broyden (1969); Fletcher (1970); Shanno (1970)
for Huber-norm minimization.
Another possibility is the CGG method proposed in the preceding section.
In the next subsections the results of the CGG method
for the velocity-stack inversion are
compared with the results of conventional
LS method and 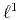 -norm IRLS method.
-norm IRLS method.
Subsections
 |
 |
 |
 | Conjugate guided gradient (CGG) method for robust inversion and its application to velocity-stack inversion |  |
![[pdf]](icons/pdf.png) |
Next: Examples on synthetic data
Up: Conjugate guided gradient (CGG)
Previous: CGG with residual and
2011-06-26
![]() that transforms
a point in a model space (velocity-stack panel)
that transforms
a point in a model space (velocity-stack panel) ![]() into a hyperbola in data space (CMP gather)
into a hyperbola in data space (CMP gather) ![]() ,
,

![]() -norm minimization,
and Guiiton and Symes (2003) used
a quasi-Newton method called limited-memory BFGS
Goldfarb (1970); Nocedal (1980); Broyden (1969); Fletcher (1970); Shanno (1970)
for Huber-norm minimization.
Another possibility is the CGG method proposed in the preceding section.
In the next subsections the results of the CGG method
for the velocity-stack inversion are
compared with the results of conventional
LS method and
-norm minimization,
and Guiiton and Symes (2003) used
a quasi-Newton method called limited-memory BFGS
Goldfarb (1970); Nocedal (1980); Broyden (1969); Fletcher (1970); Shanno (1970)
for Huber-norm minimization.
Another possibility is the CGG method proposed in the preceding section.
In the next subsections the results of the CGG method
for the velocity-stack inversion are
compared with the results of conventional
LS method and ![]() -norm IRLS method.
-norm IRLS method.