|
|
|
|
Nonstationarity: patching |
|
rabdomain
Figure 4. Domain of inputs and outputs of a two-dimensional prediction-error filter. |
|
|---|---|
|
|
|
rabtent
Figure 5. Placement of tent-like weighting function in the space of filter inputs and outputs. |

|
|---|---|
|
|
/* loop in the window */
for (i=0; i < nw; i++) {
sf_line2cart(dim, nwind, i, x);
windwt[i] = 1.;
for (j=0; j < dim; j++) {
if (x[j] >= start[j] && x[j] <= end[j]) {
w = (x[j]-mid[j])/wid[j];
windwt[i] *= SF_MAX(0.,1.-fabs(w));
} else {
windwt[i] = 0.;
}
}
}
|
In applications where triangle weights are needed on the inputs (or where we can work on a patch without having interference with edges), we can get ``triangle tent'' weights from tentn() if we set filter dimensions and lags to unity, as shown in Figure 6.
|
wind1wt
Figure 6. Window weights from tentn() with nwind=(61,19), center=(31,1), a=(1,1) . |
|
|---|---|
|
|
Triangle weighting functions
can sum to a constant
if the spacing is such that the midpoint of one triangle
is at the beginning of the next.
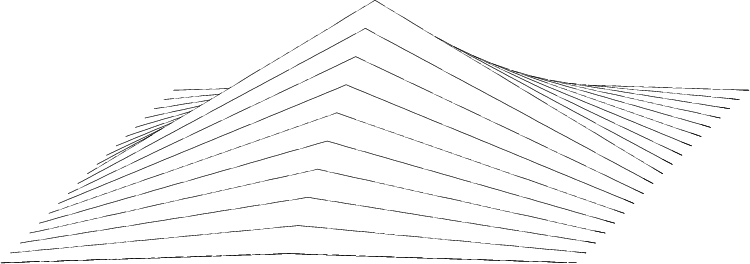
I imagined in two dimensions that something similar would happen
with shapes like Egyptian pyramids of Cheops,
![]() .
Instead,
the equation
.
Instead,
the equation
![]() which has the tent-like shape shown
in Figure 6
adds up to the constant flat top shown in Figure 7.
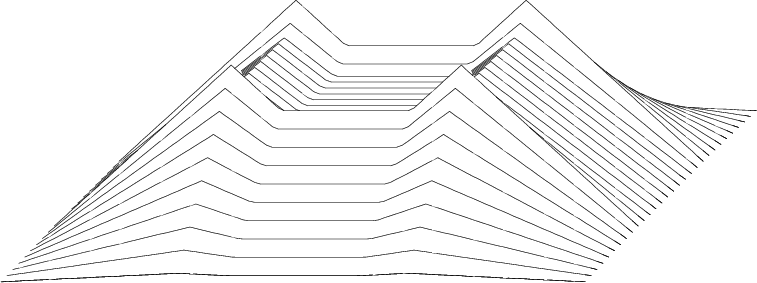
(To add interest to Figure 7,
I separated the windows by a little more than the precise matching distance.)
In practice we may chose window shapes and overlaps for
reasons other than the constancy of the sum of weights,
because mkwallwt
which has the tent-like shape shown
in Figure 6
adds up to the constant flat top shown in Figure 7.
(To add interest to Figure 7,
I separated the windows by a little more than the precise matching distance.)
In practice we may chose window shapes and overlaps for
reasons other than the constancy of the sum of weights,
because mkwallwt ![]() accounts for that.
accounts for that.
|
wall1wt
Figure 7. (Inverse) wall weights with n1=100, w1=61, k1=2, n2=30, w2=19, k2=2 |
|
|---|---|
|
|
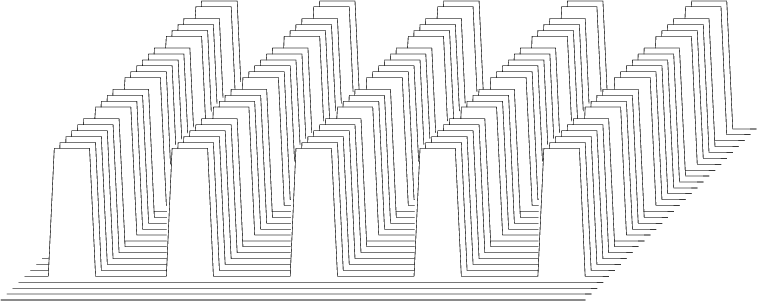
Finally is an example of filtering a plane of uniform constants with an impulse function. The impulse function is surrounded by zeros, so the filter output patches are smaller than the input patches back in Figure 3. Here in Figure 8, both axes need more window density.
|
cinloip
Figure 8. Filtering in patches Mid with the same parameters as in Figures 2 and 3. Additionally, the filter parameters are a1=11 a2=5 lag1=6 lag2=1 . Thus, windows are centered on the 1-axis and pushed back out the 2-axis. |
|
|---|---|
|
|
|
|
|
|
Nonstationarity: patching |