|
|
|
|
Multidimensional autoregression |
Sometimes we deal with small patches of data. In order that boundary phenomena not dominate the calculation intended in the central region, we need to take care that input data is not assumed to be zero beyond the interval that the data is given.
The two little triangular patches of zeros in
the convolution matrix in equation (29)
describe end conditions where it is assumed that the data ![]() vanishes before
vanishes before ![]() and after
and after ![]() .
Alternately we might not wish to make that assumption.
Thus the triangles filled with zeros could be regarded as missing data.
In this one-dimensional example,
it is easy to see that the filter, say
.
Alternately we might not wish to make that assumption.
Thus the triangles filled with zeros could be regarded as missing data.
In this one-dimensional example,
it is easy to see that the filter, say
yy->mis
should be set to true at the ends so no output
would ever be computed there.
We would like to find a general multidimensional algorithm
to correctly specify
yy->mis
around the multidimensional boundaries.
This proceeds like the missing data algorithm,
i.e. we apply a filter of all ones to a data space template that is taken
all zeros except ones at the locations of missing data,
in this case
![]() and
and ![]() .
This amounts to surrounding the original data set with some missing data.
We need padding the size of the filter on all sides.
The padded region would be filled
with ones (designating missing inputs).
Where the convolution output is nonzero, there
.
This amounts to surrounding the original data set with some missing data.
We need padding the size of the filter on all sides.
The padded region would be filled
with ones (designating missing inputs).
Where the convolution output is nonzero, there
yy->mis is set to true
denoting an output with missing inputs.
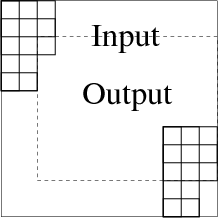
The two-dimensional case is a little more cluttered than the 1-D case
but the principle is about the same.
Figure 14 shows a larger input domain,
a ![]() filter, and a smaller output domain.
filter, and a smaller output domain.
|
rabdomain
Figure 14. Domain of inputs and outputs of a two-dimensional filter like a PEF. |
|
|---|---|
|
|
In practice, the input and output are allocated equal memory,
but the output residual is initialized to zero everywhere
and then not computed
except where shown in figure 14.
Below is module bound
to build a selector for filter outputs that should
never be examined or even computed
(because they need input data from outside the given data space).
Inputs are a filter aa
and the size of its cube na = (na(1),na(2),...).
Also input are two cube dimensions,
that of the data last used by the filter nold and
that of the filter's next intended use nd.
(nold and nd are often the same).
Module bound
begins by defining a bigger data space with room for a filter
surrounding the original data space nd on all sides.
It does this by the line nb=nd+2*na.
Then we allocate two data spaces
xx and yy of the bigger size nb
and pack many ones
in a frame of width na around the outside of xx.
The filter aa is also filled with ones.
The filter aa must be regridded for the bigger nb
data space (regridding merely changes the lag values of the ones).
Now we filter the input xx with aa getting yy.
Wherever the output is nonzero,
we have an output that has been affected by the boundary.
Such an output should not be computed.
Thus we allocate the logical mask aa->mis
(a part of the helix filter definition
in module helix ![]() )
and wherever we see a nonzero value of yy
in the output,
we designate the output as depending on missing inputs by setting
)
and wherever we see a nonzero value of yy
in the output,
we designate the output as depending on missing inputs by setting
aa->mis to true.
void bound (int dim /* number of dimensions */,
const int *nold /* old data coordinates [dim] */,
const int *nd /* new data coordinates [dim] */,
const int *na /* filter box size [dim] */,
const sf_filter aa /* helix filter */)
/*< Mark helix filter outputs where input is off data. >*/
{
int iy, my, ib, mb, i, nb[SF_MAX_DIM], ii[SF_MAX_DIM];
float *xx, *yy;
my = mb = 1;
for (i=0; i < dim; i++) {
nb[i] = nd[i] + 2*na[i]; /* nb is a bigger space. */
mb *= nb[i];
my *= nd[i];
}
xx = sf_floatalloc(mb); yy = sf_floatalloc(mb);
for (ib=0; ib < mb; ib++) {
sf_line2cart(dim, nb, ib, ii);
xx[ib] = 0.;
for (i=0; i < dim; i++)
if(ii[i]+1 <= na[i] || ii[i]+1 > nb[i]-na[i]) {
xx[ib] = 1.;
break;
}
}
sf_helicon_init( aa);
regrid(dim, nold, nb, aa);
for (i=0; i < aa->nh; i++) aa->flt[i] = 1.;
/* apply filter */
sf_helicon_lop(false, false, mb, mb, xx, yy);
regrid(dim, nb, nd, aa);
for (i=0; i < aa->nh; i++) aa->flt[i] = 0.;
aa->mis = sf_boolalloc(my); /* attach missing designation */
for (iy = 0; iy < my; iy++) { /* map to padded space */
sf_line2cart(dim, nd, iy, ii);
for (i=0; i < dim; i++) ii[i] += na[i];
ib = sf_cart2line(dim, nb, ii);
aa->mis[iy] = (bool) (yy[ib] > 0.);
}
free (xx); free (yy);
}
|
In reality one would set up the boundary conditions with module bound before identifying locations of missing data with module misinput. Both modules are based on the same concept, but the boundaries are more cluttered and confusing which is why we examined them later.
|
|
|
|
Multidimensional autoregression |