 |
 |
 |
 | Model fitting by least squares |  |
![[pdf]](icons/pdf.png) |
Next: About this document ...
Up: THE WORLD OF CONJUGATE
Previous: Inverse of a matrix
The conjugate-direction method is really a family of methods.
Mathematically, where there are 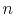 unknowns, these algorithms all
converge to the answer in
unknowns, these algorithms all
converge to the answer in 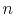 (or fewer) steps. The various methods
differ in numerical accuracy, treatment of underdetermined systems,
accuracy in treating ill-conditioned systems, space requirements, and
numbers of dot products. Technically, the method of CD used in the
cgstep module
is not the
conjugate-gradient method itself, but is equivalent to it. This
method is more properly called the conjugate-direction method
with a memory of one step. I chose this method for its clarity and
flexibility. If you would like a free introduction and summary of
conjugate-gradient methods, I particularly recommend An
Introduction to Conjugate Gradient Method Without Agonizing Pain
by Jonathon Shewchuk, which you can downloadhttp://www.cs.cmu.edu/afs/cs/project/quake/public/papers/painless-conjugate-gradient.ps.
(or fewer) steps. The various methods
differ in numerical accuracy, treatment of underdetermined systems,
accuracy in treating ill-conditioned systems, space requirements, and
numbers of dot products. Technically, the method of CD used in the
cgstep module
is not the
conjugate-gradient method itself, but is equivalent to it. This
method is more properly called the conjugate-direction method
with a memory of one step. I chose this method for its clarity and
flexibility. If you would like a free introduction and summary of
conjugate-gradient methods, I particularly recommend An
Introduction to Conjugate Gradient Method Without Agonizing Pain
by Jonathon Shewchuk, which you can downloadhttp://www.cs.cmu.edu/afs/cs/project/quake/public/papers/painless-conjugate-gradient.ps.
I suggest you skip over the remainder of this section and return
after you have seen many examples and have developed some expertise,
and have some technical problems.
The conjugate-gradient method was introduced
by Hestenes and Stiefel in 1952.
To read the standard literature and relate it to this book,
you should first realize that when I write fitting goals like
they are equivalent to minimizing the quadratic form:
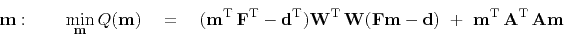 |
(114) |
The optimization theory (OT) literature starts from a minimization of
 |
(115) |
To relate equation (114) to (115)
we expand the parentheses in (114)
and abandon the constant term
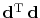 .
Then gather the quadratic term in
.
Then gather the quadratic term in 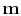 and the linear term in
and the linear term in 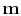 .
There are two terms linear in
.
There are two terms linear in 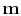 that are transposes of each other.
They are scalars so they are equal.
Thus, to invoke ``standard methods,'' you take
your problem-formulation operators
that are transposes of each other.
They are scalars so they are equal.
Thus, to invoke ``standard methods,'' you take
your problem-formulation operators 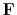 ,
, 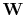 ,
, 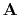 and create two subroutines that apply:
and create two subroutines that apply:
The operators 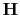 and
and  operate on model space.
Standard procedures do not require their adjoints
because
operate on model space.
Standard procedures do not require their adjoints
because 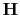 is its own adjoint and
is its own adjoint and  reduces model space to a scalar.
You can see that computing
reduces model space to a scalar.
You can see that computing  and
and  requires
one temporary space the size of data space
(whereas cgstep requires two).
requires
one temporary space the size of data space
(whereas cgstep requires two).
When people have trouble with conjugate gradients or conjugate
directions, I always refer them to the Paige and Saunders
algorithm LSQR. Methods that form  explicitly or
implicitly (including both the standard literature and the book3
method) square the condition number, that is, they are twice as
susceptible to rounding error as is LSQR. The Paige and
Saunders method is reviewed by Nolet in a geophysical context.
explicitly or
implicitly (including both the standard literature and the book3
method) square the condition number, that is, they are twice as
susceptible to rounding error as is LSQR. The Paige and
Saunders method is reviewed by Nolet in a geophysical context.
EXERCISES:
- It is possible to reject two dips with the operator:
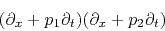 |
(118) |
This is equivalent to:
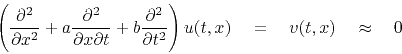 |
(119) |
where 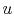 is the input signal, and
is the input signal, and 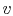 is the output signal. Show how to solve for
is the output signal. Show how to solve for 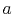 and
and 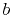 by minimizing the energy in
by minimizing the energy in 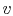 .
.
- Given
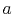 and
and 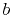 from the previous exercise, what are
from the previous exercise, what are 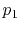 and
and  ?
?
- Reduce
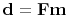 to the special case of one data point and two model points like this:
to the special case of one data point and two model points like this:
![\begin{displaymath}
d \quad =\quad
\left[
\begin{array}{cc}
2 & 1
\end{array}\right]
\left[
\begin{array}{c}
m_1
\\
m_2
\end{array}\right]
\end{displaymath}](img473.png) |
(120) |
What is the null space?
- In 1695,
150 years before Lord Kelvin's absolute temperature scale,
120 years before Sadi Carnot's PhD. thesis,
40 years before Anders Celsius,
and 20 years before Gabriel Fahrenheit,
the French physicist Guillaume Amontons,
deaf since birth,
took a mercury manometer (pressure gauge) and sealed it inside a glass pipe (a constant volume of air).
He heated it to the boiling point of water at 100
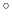 C.
As he lowered the temperature to freezing at 0
C.
As he lowered the temperature to freezing at 0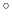 C,
he observed the pressure dropped by 25% .
He could not drop the temperature any further, but he supposed that if he could drop it further by a factor of three,
the pressure would drop to zero (the lowest possible pressure), and the temperature would have been the lowest possible temperature.
Had he lived after Anders Celsius, he might have calculated this temperature to be
C,
he observed the pressure dropped by 25% .
He could not drop the temperature any further, but he supposed that if he could drop it further by a factor of three,
the pressure would drop to zero (the lowest possible pressure), and the temperature would have been the lowest possible temperature.
Had he lived after Anders Celsius, he might have calculated this temperature to be 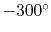 C (Celsius).
Absolute zero is now known to be
C (Celsius).
Absolute zero is now known to be 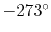 C.
C.
It is your job to be Amontons' lab assistant.
You make your i-th measurement of temperature 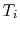 with Issac
Newton's thermometer;
and you measure pressure
with Issac
Newton's thermometer;
and you measure pressure 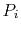 and volume
and volume 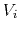 in the metric system.
Amontons needs you to fit his data with the regression
in the metric system.
Amontons needs you to fit his data with the regression
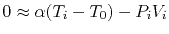 and calculate the temperature shift
and calculate the temperature shift 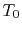 that Newton should have made when he defined his temperature scale.
Do not solve this problem!
Instead,
cast it in the form of equation (
that Newton should have made when he defined his temperature scale.
Do not solve this problem!
Instead,
cast it in the form of equation (![[*]](icons/crossref.png) ),
identifying the data
),
identifying the data 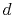 and the two column vectors
and the two column vectors 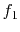 and
and 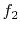 that are the fitting functions.
Relate the model parameters
that are the fitting functions.
Relate the model parameters 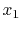 and
and 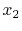 to the physical parameters
to the physical parameters 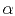 and
and 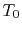 .
Suppose you make ALL your measurements at room temperature,
can you find
.
Suppose you make ALL your measurements at room temperature,
can you find 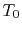 ?
Why or why not?
?
Why or why not?
- One way to remove a mean value
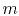 from signal
from signal 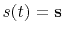 is with the fitting goal
is with the fitting goal
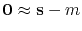 .
What operator matrix is involved?
.
What operator matrix is involved?
- What linear operator subroutine from Chapter
![[*]](icons/crossref.png) can be used for finding the mean?
can be used for finding the mean?
- How many CD iterations should be required to get the exact mean value?
- Write a mathematical expression for finding the mean by the CG method.
 |
 |
 |
 | Model fitting by least squares |  |
![[pdf]](icons/pdf.png) |
Next: About this document ...
Up: THE WORLD OF CONJUGATE
Previous: Inverse of a matrix
2014-12-01
![]() explicitly or
implicitly (including both the standard literature and the book3
method) square the condition number, that is, they are twice as
susceptible to rounding error as is LSQR. The Paige and
Saunders method is reviewed by Nolet in a geophysical context.
explicitly or
implicitly (including both the standard literature and the book3
method) square the condition number, that is, they are twice as
susceptible to rounding error as is LSQR. The Paige and
Saunders method is reviewed by Nolet in a geophysical context.
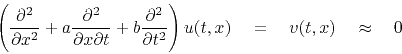
![\begin{displaymath}
d \quad =\quad
\left[
\begin{array}{cc}
2 & 1
\end{array}\right]
\left[
\begin{array}{c}
m_1
\\
m_2
\end{array}\right]
\end{displaymath}](img473.png)
![]() with Issac
Newton's thermometer;
and you measure pressure
with Issac
Newton's thermometer;
and you measure pressure ![]() and volume
and volume ![]() in the metric system.
Amontons needs you to fit his data with the regression
in the metric system.
Amontons needs you to fit his data with the regression
![]() and calculate the temperature shift
and calculate the temperature shift ![]() that Newton should have made when he defined his temperature scale.
Do not solve this problem!
Instead,
cast it in the form of equation (
that Newton should have made when he defined his temperature scale.
Do not solve this problem!
Instead,
cast it in the form of equation (![]() ),
identifying the data
),
identifying the data ![]() and the two column vectors
and the two column vectors ![]() and
and ![]() that are the fitting functions.
Relate the model parameters
that are the fitting functions.
Relate the model parameters ![]() and
and ![]() to the physical parameters
to the physical parameters ![]() and
and ![]() .
Suppose you make ALL your measurements at room temperature,
can you find
.
Suppose you make ALL your measurements at room temperature,
can you find ![]() ?
Why or why not?
?
Why or why not?