|
|
|
|
The helical coordinate |
Let us have an example.
Consider a filter like the familiar time derivative ![]() , except
let us down weight the
, except
let us down weight the ![]() a tiny bit, say
a tiny bit, say ![]() where
where ![]() .
Now,
the filter
.
Now,
the filter ![]() has a spectrum
has a spectrum
![]() with autocorrelation
coefficients
with autocorrelation
coefficients
![]() that look a lot like a second derivative,
but it is a tiny bit bigger in the middle.
Two different waveforms,
that look a lot like a second derivative,
but it is a tiny bit bigger in the middle.
Two different waveforms, ![]() and its time reverse
both have the same autocorrelation.
In principle,
spectral factorization could give us both
and its time reverse
both have the same autocorrelation.
In principle,
spectral factorization could give us both ![]() and
and ![]() ,
but we always want only the one that is CCI,
which is the one we get from Kolmogoroff.
The bad one is weaker on its first pulse.
Its inverse is not causal.
Following are two expressions for the filter inverse to
,
but we always want only the one that is CCI,
which is the one we get from Kolmogoroff.
The bad one is weaker on its first pulse.
Its inverse is not causal.
Following are two expressions for the filter inverse to ![]() ,
the first divergent
(filter coefficients at infinite lag are infinitely strong),
the second convergent but noncausal.
,
the first divergent
(filter coefficients at infinite lag are infinitely strong),
the second convergent but noncausal.
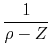 |
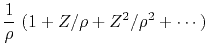 |
(16) | |
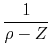 |
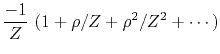 |
(17) |
We begin with a power spectrum, and our goal is to find a CCI filter with that spectrum. If we input to the filter an infinite sequence of random numbers (white noise), we should output something with the original power spectrum.
We easily inverse Fourier transform the square root of the power spectrum,
getting a symmetrical time function, but
we need a function that vanishes before ![]() .
On the other hand,
if we already had a causal filter with the correct spectrum
we could manufacture many others.
To do so,
all we need is a family of delay operators for convolution.
A pure delay filter does not change the spectrum of anything--same for frequency-dependent delay operators.
Here is an example of a frequency-dependent delay operator:
First,
convolve with (1,2) and then deconvolve with (2,1).
Both these have the same amplitude spectrum,
so the ratio has a unit amplitude (and nontrivial phase).
If you multiply
.
On the other hand,
if we already had a causal filter with the correct spectrum
we could manufacture many others.
To do so,
all we need is a family of delay operators for convolution.
A pure delay filter does not change the spectrum of anything--same for frequency-dependent delay operators.
Here is an example of a frequency-dependent delay operator:
First,
convolve with (1,2) and then deconvolve with (2,1).
Both these have the same amplitude spectrum,
so the ratio has a unit amplitude (and nontrivial phase).
If you multiply
![]() , by its Fourier conjugate
(replace
, by its Fourier conjugate
(replace ![]() by
by ![]() ) the resulting spectrum is 1 for all
) the resulting spectrum is 1 for all ![]() .
.
Anything with a nature to delay is death to CCI.
The CCI has its energy as close as possible to ![]() .
More formally, my first book,
FGDP
proves the CCI filter
has for all time
.
More formally, my first book,
FGDP
proves the CCI filter
has for all time ![]() more energy between
more energy between ![]() and
and ![]() than any other filter with the same spectrum.
than any other filter with the same spectrum.
Spectra can be factorized by an amazingly wide variety of techniques, each of which gives you a different insight into this strange beast. Spectra can be factorized by factoring polynomials, inserting power series into other power series, solving least squares problems, and by taking logarithms and exponentials in the Fourier domain. I have coded most of of these methods, and find each seemingly unrelated to the others.
Theorems in Fourier analysis can be interpreted physically in two
different ways, one as given, and the other with time and frequency reversed.
For example, convolution in one domain amounts to multiplication in the other.
If we express the CCI concept with reversed domains,
instead of saying the ``energy comes as quick as possible after ![]() ''
we would say ``the frequency function is as close to
''
we would say ``the frequency function is as close to ![]() as possible.''
In other words, it is minimally wiggly with time.
Most applications of spectral factorization begin with a spectrum,
a real, positive function of frequency.
I once recognized the opposite case
and achieved minor fame by starting with a real, positive function of space,
a total magnetic field
as possible.''
In other words, it is minimally wiggly with time.
Most applications of spectral factorization begin with a spectrum,
a real, positive function of frequency.
I once recognized the opposite case
and achieved minor fame by starting with a real, positive function of space,
a total magnetic field
![]() measured along the
measured along the ![]() -axis;
and I reconstructed the magnetic field components
-axis;
and I reconstructed the magnetic field components ![]() and
and ![]() that were minimally wiggly in space (FGDP, page 61).
that were minimally wiggly in space (FGDP, page 61).
|
|
|
|
The helical coordinate |