 |
 |
 |
 | Basic operators and adjoints |  |
![[pdf]](icons/pdf.png) |
Next: Nearest-neighbor coordinates
Up: FAMILIAR OPERATORS
Previous: Zero padding is the
Here, we examine an example of the general idea that
adjoints of products are reverse-ordered products of adjoints.
For this example, we use the Fourier transformation.
No details of Fourier transformation are given here,
and we merely use it as an example of a square matrix 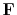 .
We denote the complex-conjugate transpose (or adjoint) matrix
with a prime,
i.e.,
.
We denote the complex-conjugate transpose (or adjoint) matrix
with a prime,
i.e., 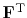 .
The adjoint arises naturally whenever we consider energy.
The statement that Fourier transforms conserve energy is
.
The adjoint arises naturally whenever we consider energy.
The statement that Fourier transforms conserve energy is
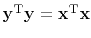 where
where
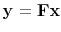 .
Substituting gives
.
Substituting gives
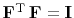 , which shows that
the inverse matrix to Fourier transform
happens to be the complex conjugate of the transpose of
, which shows that
the inverse matrix to Fourier transform
happens to be the complex conjugate of the transpose of 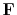 .
.
With Fourier transforms,
zero padding and truncation are especially prevalent.
Most modules transform a dataset of length of 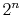 ;
whereas, dataset lengths are often of length
;
whereas, dataset lengths are often of length  .
The practical approach is therefore to pad given data with zeros.
Padding followed by Fourier transformation
.
The practical approach is therefore to pad given data with zeros.
Padding followed by Fourier transformation  can be expressed in matrix algebra as
can be expressed in matrix algebra as
![\begin{displaymath}
{\rm Program} \eq
\bold F \
\left[
\begin{array}{c}
\bold I \\
\bold 0
\end{array} \right]
\end{displaymath}](img66.png) |
(13) |
According to matrix algebra, the transpose of a product,
say
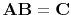 ,
is the product
,
is the product
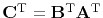 in reverse order.
Therefore, the adjoint routine is given by
in reverse order.
Therefore, the adjoint routine is given by
![\begin{displaymath}
{\rm Program}\T \eq
\left[
\begin{array}{cc}
\bold I & \bold 0
\end{array} \right]
\
\bold F\T
\end{displaymath}](img69.png) |
(14) |
Thus, the adjoint routine
truncates the data after the inverse Fourier transform.
This concrete example illustrates that common sense often represents
the mathematical abstraction
that adjoints of products are reverse-ordered products of adjoints.
It is also nice to see a formal mathematical notation
for a practical necessity.
Making an approximation need not lead to the collapse of all precise analysis.
 |
 |
 |
 | Basic operators and adjoints |  |
![[pdf]](icons/pdf.png) |
Next: Nearest-neighbor coordinates
Up: FAMILIAR OPERATORS
Previous: Zero padding is the
2014-09-27
![]() ;
whereas, dataset lengths are often of length
;
whereas, dataset lengths are often of length ![]() .
The practical approach is therefore to pad given data with zeros.
Padding followed by Fourier transformation
.
The practical approach is therefore to pad given data with zeros.
Padding followed by Fourier transformation ![]() can be expressed in matrix algebra as
can be expressed in matrix algebra as
![\begin{displaymath}
{\rm Program} \eq
\bold F \
\left[
\begin{array}{c}
\bold I \\
\bold 0
\end{array} \right]
\end{displaymath}](img66.png)