 |
 |
 |
 | Basic operators and adjoints |  |
![[pdf]](icons/pdf.png) |
Next: About this document ...
Up: ADJOINT DEFINED: DOT-PRODUCT TEST
Previous: The word ``adjoint''
A common practical task is to fit a vector of observed data
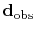 to some modeled data
to some modeled data
 by the adjustment of components in a vector of model parameters
by the adjustment of components in a vector of model parameters 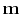 .
.
 |
(42) |
A huge volume of literature establishes theory for two estimates
of the model,
 and
and
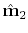 , where
, where
Some reasons for the literature being huge are the
many questions
about the existence, quality, and cost
of the inverse operators.
Let us quickly see why these two solutions are reasonable.
Inserting equation (42)
into equation (43),
and inserting equation (44)
into equation (42),
we get the reasonable statements:
Equation (45) says the estimate
 gives the correct model
gives the correct model 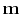 if you start from the modeled data.
Equation (46) says the model estimate
if you start from the modeled data.
Equation (46) says the model estimate
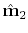 gives the modeled data if we derive
gives the modeled data if we derive
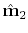 from the modeled data.
Both these statements are delightful.
Now, let us return to the problem of the inverse matrices.
from the modeled data.
Both these statements are delightful.
Now, let us return to the problem of the inverse matrices.
Normally, a rectangular matrix does not have an inverse.
Surprising things often happen, but commonly,
when 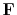 is a tall matrix
(more data values than model values),
then the matrix for finding
is a tall matrix
(more data values than model values),
then the matrix for finding
 is invertible while that for finding
is invertible while that for finding
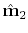 is not;
and when the matrix is wide instead of tall
(the number of data values is less than the number of model values),
it is the other way around.
In many applications neither
is not;
and when the matrix is wide instead of tall
(the number of data values is less than the number of model values),
it is the other way around.
In many applications neither
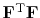 nor
nor
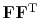 is invertible. This difficulty is
solved by ``damping'' as we see in later chapters.
If it happens that
is invertible. This difficulty is
solved by ``damping'' as we see in later chapters.
If it happens that
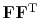 or
or
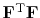 equals
equals 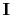 (unitary operator),
then the adjoint operator
(unitary operator),
then the adjoint operator 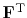 is the inverse
is the inverse 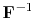 by either equation (43) or (44).
by either equation (43) or (44).
Current computational power limits matrix inversion
jobs to about 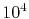 variables.
This book specializes in big problems,
those with more than about
variables.
This book specializes in big problems,
those with more than about 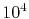 variables.
The iterative methods we learn here for giant problems
are also excellent for smaller problems;
therefore we rarely here speak of inverse matrices
or worry much if neither
variables.
The iterative methods we learn here for giant problems
are also excellent for smaller problems;
therefore we rarely here speak of inverse matrices
or worry much if neither
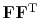 nor
nor
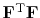 is an identity.
is an identity.
EXERCISES:
- Consider the matrix
![\begin{displaymath}
\left[
\begin{array}{cccccccc}
1 & 0 & 0 & 0 & 0 & 0 & 0 ...
...0 & 1 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 1
\end{array} \right]
\end{displaymath}](img213.png) |
(47) |
and others like it with 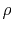 in other locations.
Show what combination of these matrices will represent
the leaky integration matrix
in equation (19). What is the adjoint?
in other locations.
Show what combination of these matrices will represent
the leaky integration matrix
in equation (19). What is the adjoint?
- Modify the calculation in Figure 5 so that there is
a triangle waveform on the bottom row.
- Notice that the triangle waveform is not time aligned
with the input in2.
Force time alignment with the operator
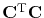 or
or
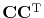 .
.
- Modify leakint
by changing the diagonal to contain
1/2 instead of 1.
Notice how time alignment changes in Figure 5.
- Suppose a linear operator
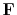 has
its input in the discrete domain and
its output in the continuum.
How does the operator resemble a matrix?
Describe the operator
has
its input in the discrete domain and
its output in the continuum.
How does the operator resemble a matrix?
Describe the operator 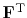 that has
its input in the discrete domain and
its output in the continuum.
To which do you apply the words
``scales and adds some functions,''
and to which do you apply the words
``does a bunch of integrals''?
What are the integrands?
that has
its input in the discrete domain and
its output in the continuum.
To which do you apply the words
``scales and adds some functions,''
and to which do you apply the words
``does a bunch of integrals''?
What are the integrands?
 |
 |
 |
 | Basic operators and adjoints |  |
![[pdf]](icons/pdf.png) |
Next: About this document ...
Up: ADJOINT DEFINED: DOT-PRODUCT TEST
Previous: The word ``adjoint''
2014-09-27
![]() is a tall matrix
(more data values than model values),
then the matrix for finding
is a tall matrix
(more data values than model values),
then the matrix for finding
![]() is invertible while that for finding
is invertible while that for finding
![]() is not;
and when the matrix is wide instead of tall
(the number of data values is less than the number of model values),
it is the other way around.
In many applications neither
is not;
and when the matrix is wide instead of tall
(the number of data values is less than the number of model values),
it is the other way around.
In many applications neither
![]() nor
nor
![]() is invertible. This difficulty is
solved by ``damping'' as we see in later chapters.
If it happens that
is invertible. This difficulty is
solved by ``damping'' as we see in later chapters.
If it happens that
![]() or
or
![]() equals
equals ![]() (unitary operator),
then the adjoint operator
(unitary operator),
then the adjoint operator ![]() is the inverse
is the inverse ![]() by either equation (43) or (44).
by either equation (43) or (44).
![]() variables.
This book specializes in big problems,
those with more than about
variables.
This book specializes in big problems,
those with more than about ![]() variables.
The iterative methods we learn here for giant problems
are also excellent for smaller problems;
therefore we rarely here speak of inverse matrices
or worry much if neither
variables.
The iterative methods we learn here for giant problems
are also excellent for smaller problems;
therefore we rarely here speak of inverse matrices
or worry much if neither
![]() nor
nor
![]() is an identity.
is an identity.
![\begin{displaymath}
\left[
\begin{array}{cccccccc}
1 & 0 & 0 & 0 & 0 & 0 & 0 ...
...0 & 1 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 1
\end{array} \right]
\end{displaymath}](img213.png)