 |
 |
 |
 | Basic operators and adjoints |  |
![[pdf]](icons/pdf.png) |
Next: Smoothing with box and
Up: FAMILIAR OPERATORS
Previous: Backsolving, polynomial division and
Many geophysical measurements contain
very low-frequency noise called ``drift.''
For example, it might take some months to survey the depth of a lake.
Meanwhile, rainfall or evaporation could change the lake level so that
new survey lines become inconsistent with old ones.
Likewise, gravimeters are sensitive to atmospheric pressure,
which changes with the weather.
A magnetic survey of an archeological site would need to contend
with the fact that the Earth's main magnetic field is changing randomly
through time while the survey is being done.
Such noise is sometimes called ``secular noise.''
The simplest way to eliminate low-frequency noise is
to take a time derivative.
A disadvantage is that the derivative
changes the waveform
from a pulse to a doublet (finite difference).
Here we examine the most basic low-cut filter.
It preserves the waveform at high frequencies,
it has an adjustable parameter
for choosing the bandwidth of the low cut,
and it is causal (uses the past but not the future).
We make a causal low-cut filter (high-pass filter) by
two stages that can be done in either order.
- Apply a time derivative, actually a finite
difference, convolving the data with
 .
.
- Do a leaky integration dividing by
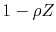 where numerically,
where numerically,
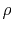 is slightly less than unity.
is slightly less than unity.
The convolution with  ensures the zero frequency is removed.
The leaky integration almost undoes the differentiation
but cannot restore the zero frequency.
Adjusting the numerical value of
ensures the zero frequency is removed.
The leaky integration almost undoes the differentiation
but cannot restore the zero frequency.
Adjusting the numerical value of 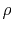 has interesting effects
in the time domain and in the frequency domain.
Convolving the finite difference
has interesting effects
in the time domain and in the frequency domain.
Convolving the finite difference  with the leaky integration
with the leaky integration
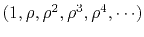 gives the result:
gives the result:
Rearranging, it becomes:
Because 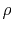 is a tiny bit less than one,
is a tiny bit less than one,
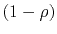 is a small number.
Thus, our filter is an impulse followed by the negative
of a weak decaying exponential
is a small number.
Thus, our filter is an impulse followed by the negative
of a weak decaying exponential 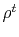 .
If you prefer a time-symmetric (phaseless) filter,
you could follow this one by its time reverse.
.
If you prefer a time-symmetric (phaseless) filter,
you could follow this one by its time reverse.
Roughly speaking, the cut-off frequency of the filter corresponds
to matching one wavelength to the exponential decay time.
More formally,
the Fourier domain representation of this filter is
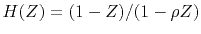 ,
where
,
where 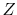 is the unit-delay operator is
is the unit-delay operator is
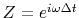 ,
and where
,
and where 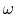 is the frequency.
The spectral response of the filter is
is the frequency.
The spectral response of the filter is 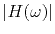 .
Were we to plot this function, we would see it is nearly 1
everywhere except in a small region near
.
Were we to plot this function, we would see it is nearly 1
everywhere except in a small region near 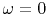 where it becomes tiny.
Figure 6 compares a low-cut filter to a finite
difference.
where it becomes tiny.
Figure 6 compares a low-cut filter to a finite
difference.
|
|---|
galocut
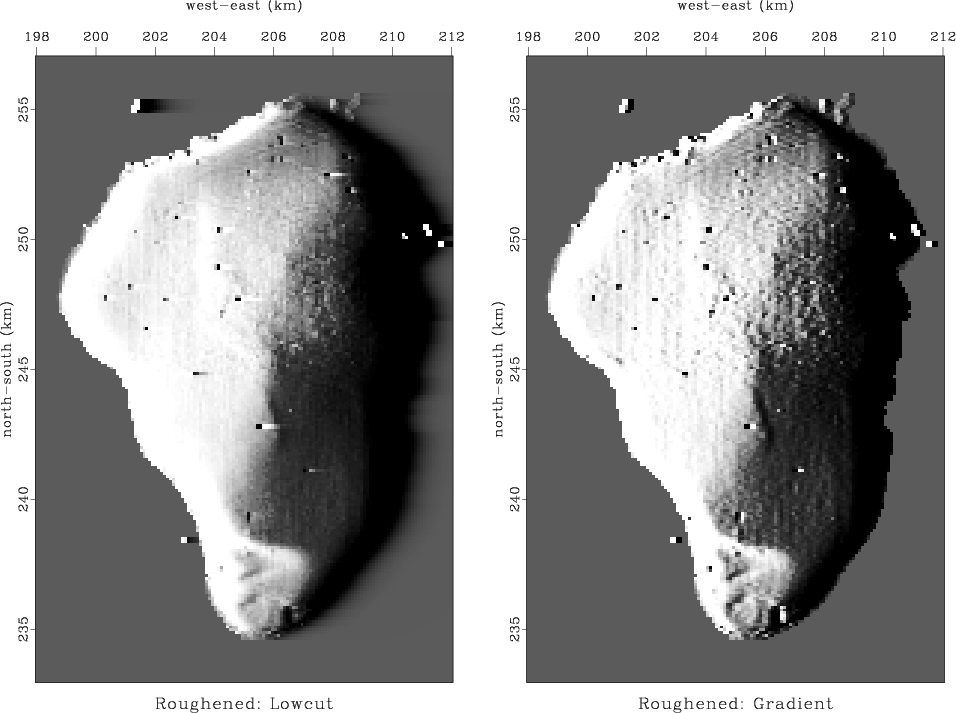
Figure 6.
The depth of the Sea of Galilee after roughening.
On the left, the smoothing is done by low-cut
filtering on the horizontal axis.
On the right it is a finite difference.
We see which is which because of a few scattered impulses
(navigation failure) outside the lake.
Both results solve the problem of Figure 3
that it is too smooth to see interesting features.
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|
 |
 |
 |
 | Basic operators and adjoints |  |
![[pdf]](icons/pdf.png) |
Next: Smoothing with box and
Up: FAMILIAR OPERATORS
Previous: Backsolving, polynomial division and
2014-09-27
![]() ,
where
,
where ![]() is the unit-delay operator is
is the unit-delay operator is
![]() ,
and where
,
and where ![]() is the frequency.
The spectral response of the filter is
is the frequency.
The spectral response of the filter is ![]() .
Were we to plot this function, we would see it is nearly 1
everywhere except in a small region near
.
Were we to plot this function, we would see it is nearly 1
everywhere except in a small region near ![]() where it becomes tiny.
Figure 6 compares a low-cut filter to a finite
difference.
where it becomes tiny.
Figure 6 compares a low-cut filter to a finite
difference.
