|
|
|
|
Basic operators and adjoints |
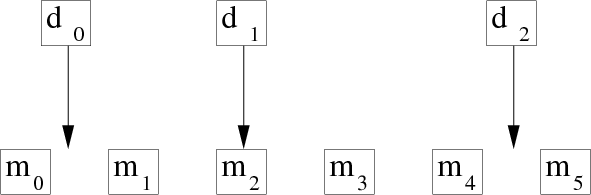
The linear interpolation operator is much like the binning operator but a little fancier. When we perform the forward operation, we take each data coordinate and see which two model bin centers bracket it. Then, we pick up the two bracketing model values and weight each in proportion to their nearness to the data coordinate, and add them to get the data value (ordinate). The adjoint operation is adding a data value back into the model vector; using the same two weights, the adjoint distributes the data ordinate value between the two nearest bins in the model vector. For example, suppose we have a data point near each end of the model and a third data point exactly in the middle. Then, for a model space 6 points long, as shown in Figure 4, we have the operator in equation (16).
|
helgerud
Figure 4. Uniformly sampled model space and irregularly sampled data space corresponding to equation (16). |
|
|---|---|
|
|
Module lint1 does linear interpolation and its adjoint.
In Chapters ![]() and
and ![]() ,
we build inverse operators.
,
we build inverse operators.
for (id=0; id < nd; id++) {
f = (coord[id]-o1)/d1;
im=floorf(f);
if (0 <= im && im < nm-1) {
fx=f-im;
gx=1.-fx;
if(adj) {
mm[im] += gx * dd[id];
mm[im+1] += fx * dd[id];
} else {
dd[id] += gx * mm[im] + fx * mm[im+1];
}
}
}
|
|
|
|
|
Basic operators and adjoints |