Waves and Fourier sums

Common signals

Figure 2 shows some common signals and their autocorrelations. Figure 3 shows the cosine transforms of the autocorrelations. Cosine transform takes us from time to frequency and it also takes us from frequency to time. Thus, transform pairs in Figure 3 are sometimes more comprehensible if you interchange time and frequency. The various signals are given names in the figures, and a description of each follows:

autocor
Figure 2. Common signals and one side of their autocorrelations.

spectra
Figure 3. Autocorrelations and their cosine transforms, i.e., the (energy) spectra of the common signals.

cos

The theoretical spectrum of a sinusoid is an impulse, but the sinusoid was truncated (multiplied by a rectangle function). The autocorrelation is a sinusoid under a triangle, and its spectrum is a broadened impulse (which can be shown to be a narrow sinc-squared function).

sinc

The sinc function is 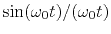$\sin(\omega_0 t)/(\omega_0 t)$. Its autocorrelation is another sinc function, and its spectrum is a rectangle function. Here the rectangle is corrupted slightly by ``Gibbs sidelobes,'' which result from the time truncation of the original sinc.

wide box

A wide rectangle function has a wide triangle function for an autocorrelation and a narrow sinc-squared spectrum.

narrow box

A narrow rectangle has a wide sinc-squared spectrum.

twin

Two pulses.

2 boxes

Two separated narrow boxes have the spectrum of one of them, but this spectrum is modulated (multiplied) by a sinusoidal function of frequency, where the modulation frequency measures the time separation of the narrow boxes. (An oscillation seen in the frequency domain is sometimes called a ``quefrency.'')

comb

Fine-toothed-comb functions are like rectangle functions with a lower Nyquist frequency. Coarse-toothed-comb functions have a spectrum which is a fine-toothed comb.

exponential

The autocorrelation of a transient exponential function is a double-sided exponential function. The spectrum (energy) is a Cauchy function, 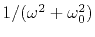$1/(\omega^2+\omega_0^2)$. The curious thing about the Cauchy function is that the amplitude spectrum diminishes inversely with frequency to the first power; hence, over an infinite frequency axis, the function has infinite integral. The sharp edge at the onset of the transient exponential has much high-frequency energy.

Gauss

The autocorrelation of a Gaussian function is another Gaussian, and the spectrum is also a Gaussian.

random

Random numbers have an autocorrelation that is an impulse surrounded by some short grass. The spectrum is positive random numbers.

smoothed random

Smoothed random numbers are much the same as random numbers, but their spectral bandwidth is limited.

Waves and Fourier sums